E-mail alert
Rss
Analytical solution for Non-Darcian effect on transient confined-unconfined flow in a confined aquifer
-
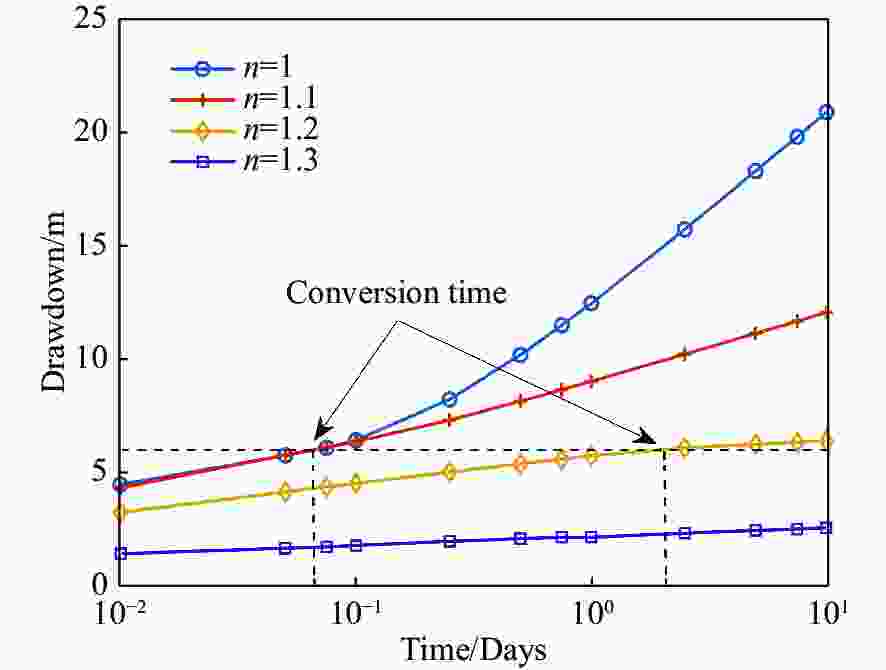
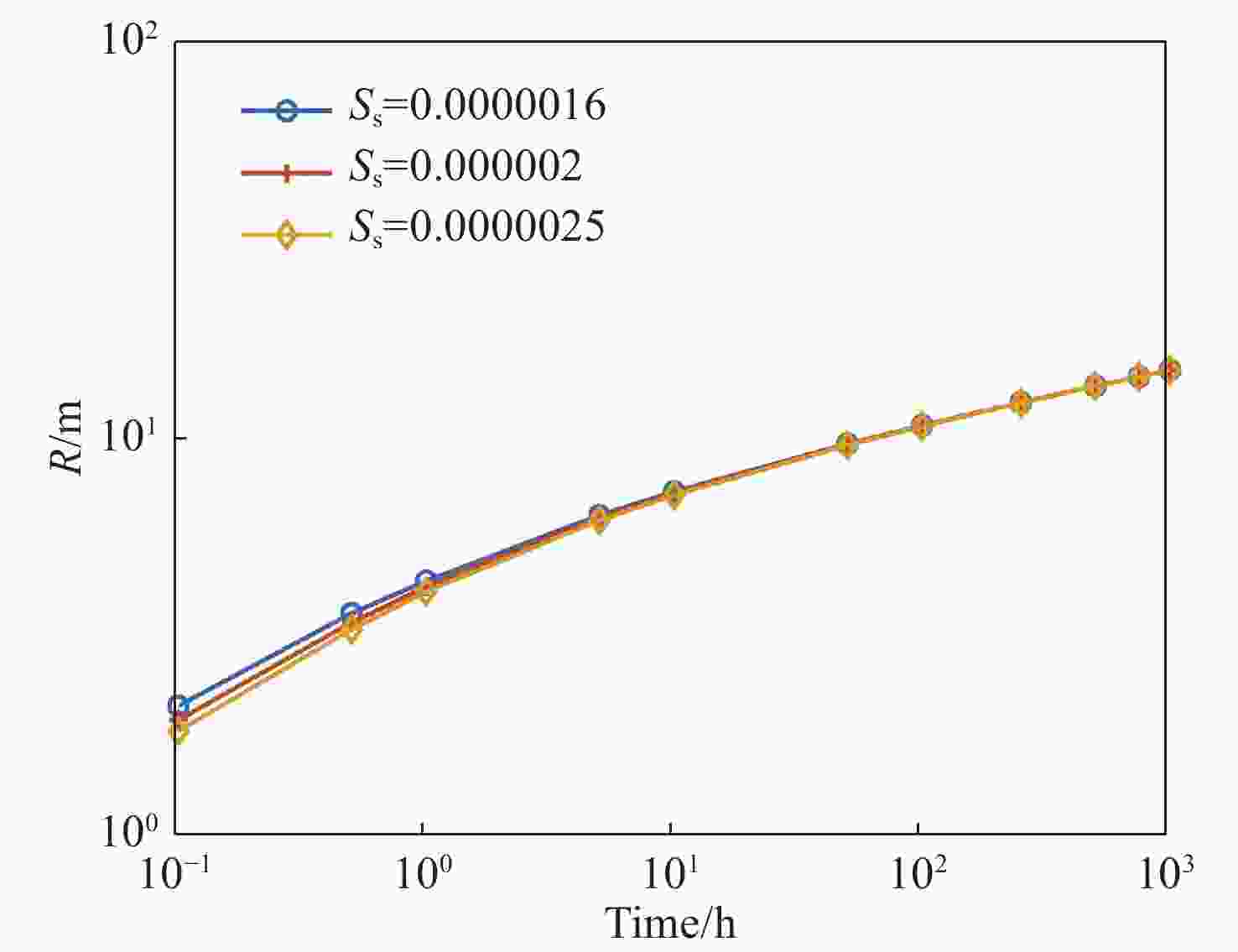
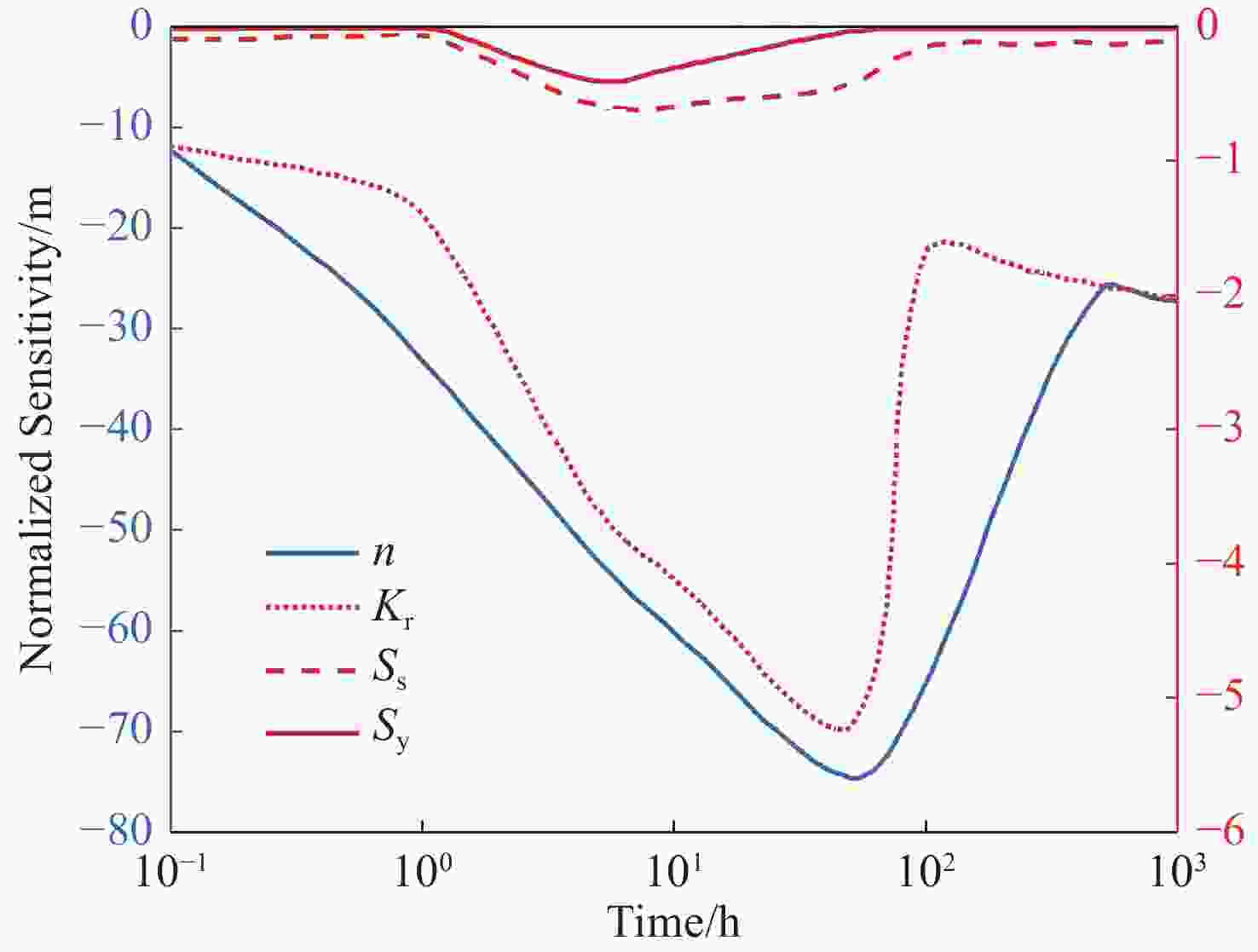
Abstract: This paper presents a new analytical solution to investigate the mechanism of transient confined-unconfined flow in a confined aquifer induced by pumping with a large rate during mine drainage. The study focuses on understanding the impact of non-Darcian effect on flow towards a fully penetrated pumping well. The nonlinear relationship between specific discharge and the hydraulic gradient is described using Izbash's equation. A novel approximate method is developed to linearize the mathematical model, and the solution is derived using the Boltzmann transform. The proposed solution is validated by comparing it with previous works. The findings indicate that increased non-Darcian index, quasi-hydraulic conductivity, and specific storage have negatively affect the development of the unconfined region and aquifer drawdown, as greater turbulence flow accelerates recharge to the pumping well. Drawdown is found to be sensitive to the non-Darcian index, quasi-hydraulic conductivity, while it is unaffected by specific yield and specific storage. The conclusions provide valuable insights for mine drainage and the application of geological and hydrological conditions.
-
Key words:
- Non-Darcian flow /
- Izbash equation /
- Boltzmann transform /
- Sensitivity analysis
-
Figure 1. A schematic diagram of the transient confined-unconfined flow towards a fully penetrating well in a confined aquifer.
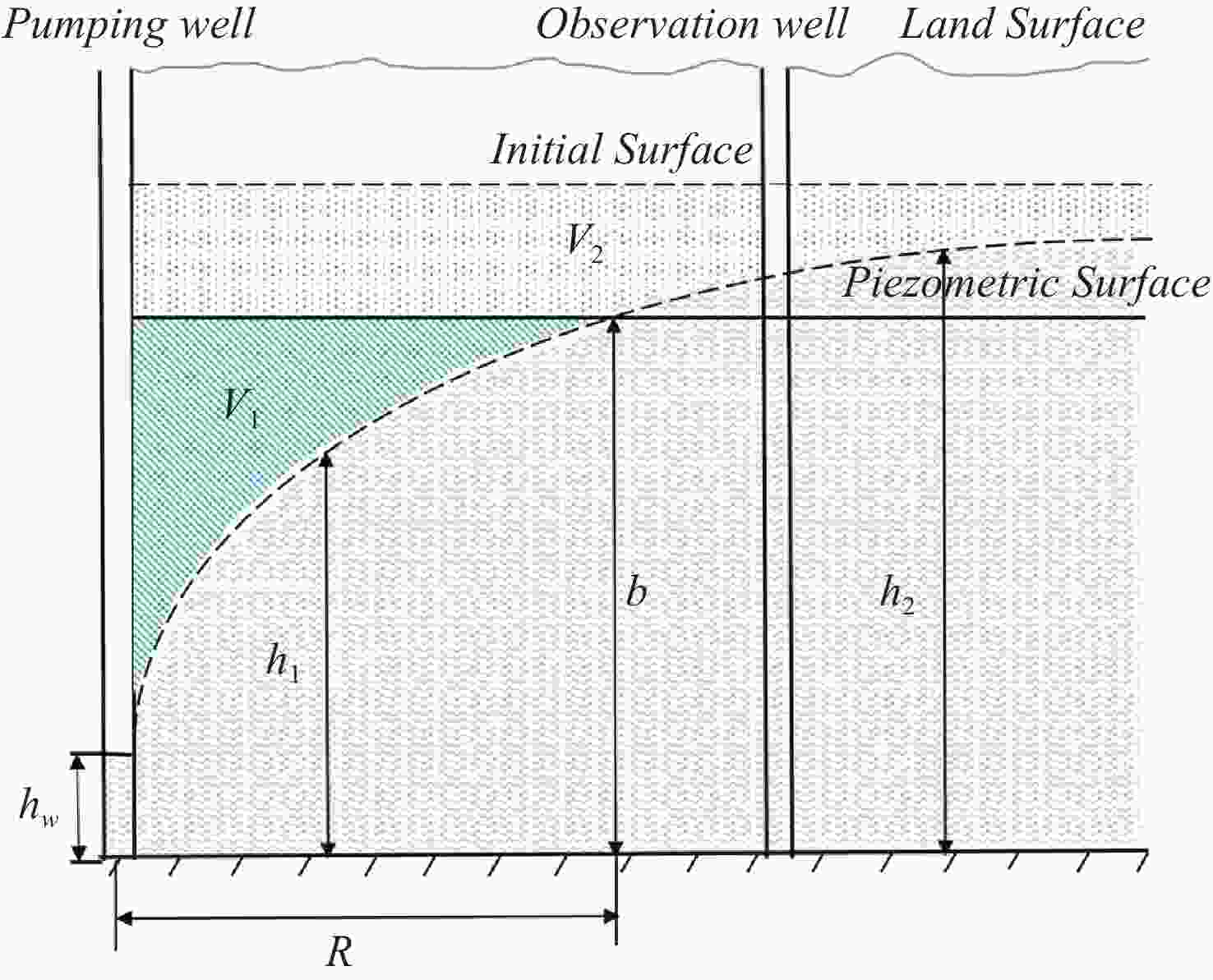
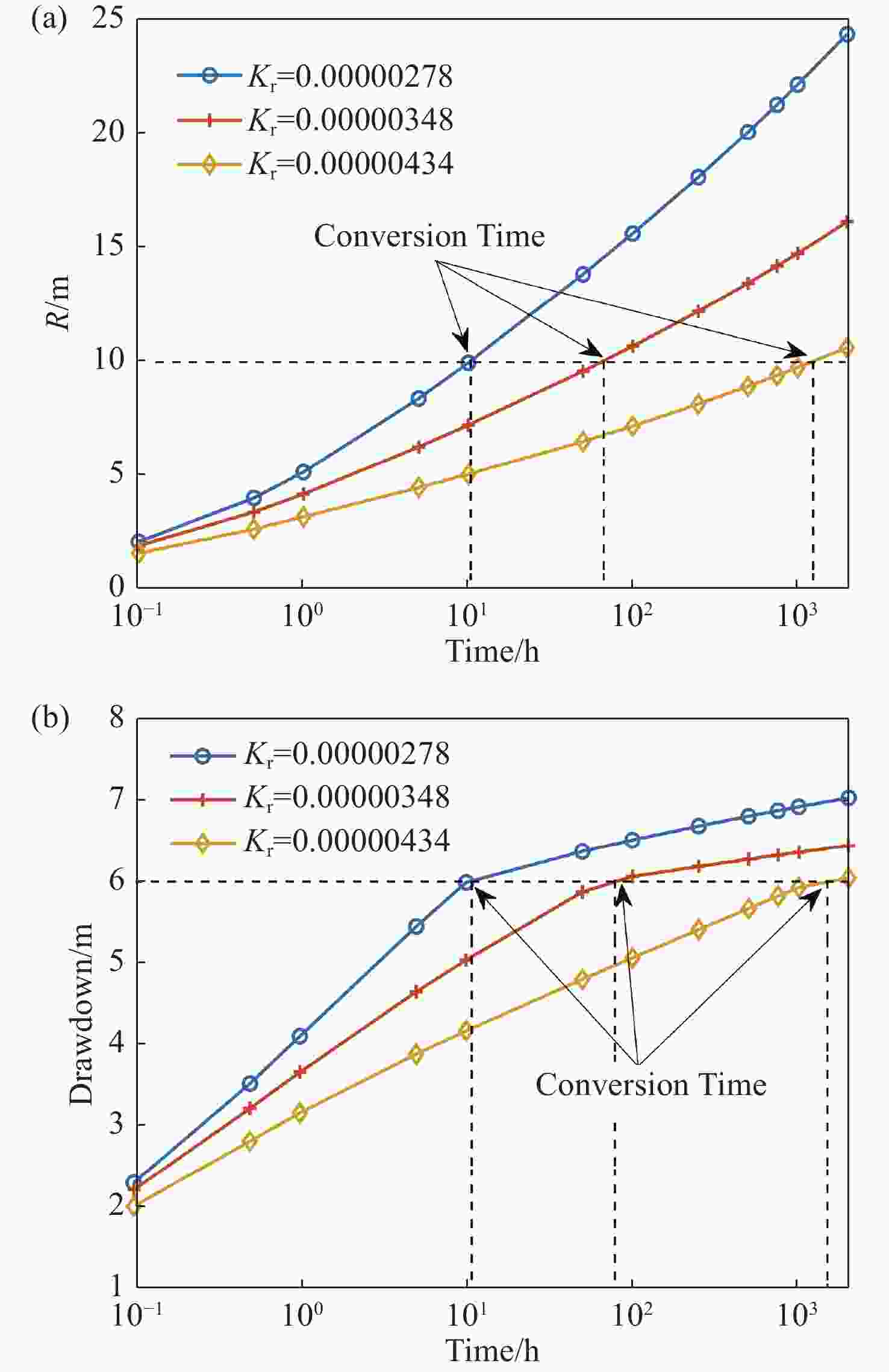
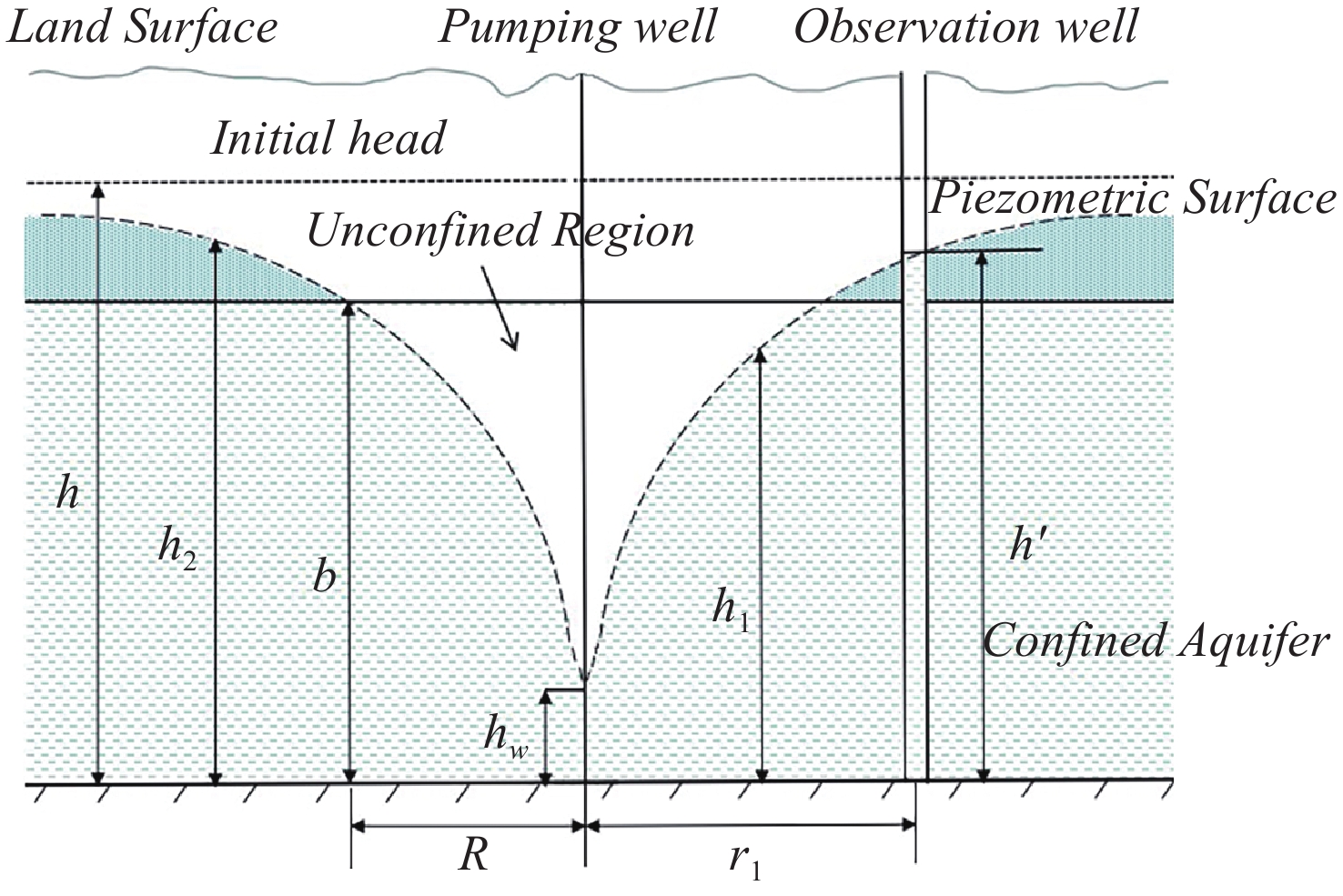
Figure 2. Change of groundwater storage during the confined-unconfined conversion (after Hu and Chen, 2008).
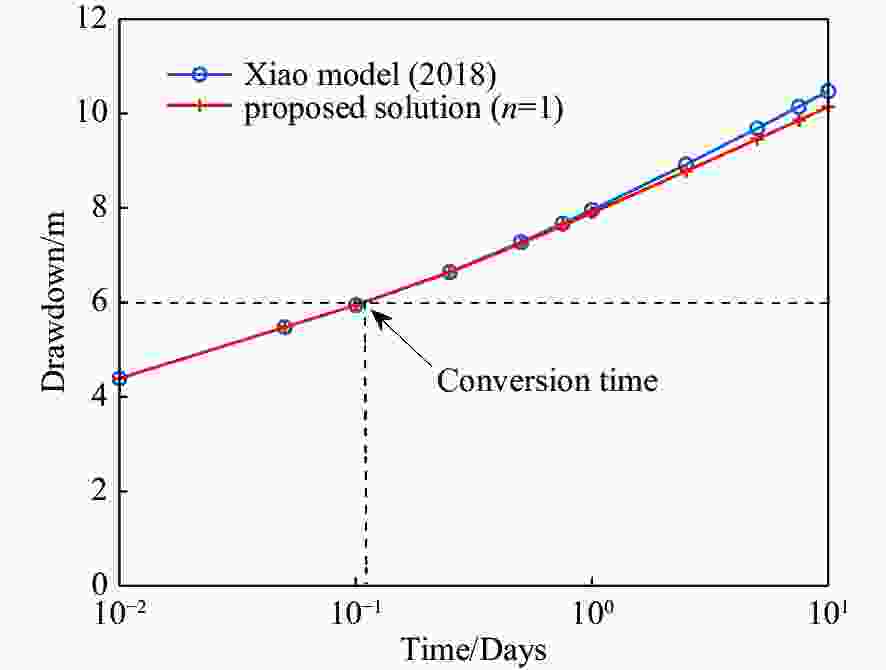
Figure 3. Comparison of time-Drawdown curves with Xiao's model
Notes: Under the condition of $ Q=0.026\;{\mathrm{m}}^{3}/\mathrm{s} $, ${K}_{r}= $$ 0.0000695\;\mathrm{m}/\mathrm{s}$, ${S}_{s}=0.000002\;{\mathrm{m}}^{-1}$, $ {S}_{y}=0.3 $, $ b=30\;\mathrm{m} $, $ {h}_{0}=36\;\mathrm{m} $, $ r=10\;\mathrm{m} $ and $ n=1 $ in semi-log scales
Figure 4. Time-Drawdown behavior for different index
$ n $ Notes: With $ Q=0.04\;{\mathrm{m}}^{3}/\mathrm{s} $, ${K}_{r}=0.0000278\;\mathrm{m}/\mathrm{s}$, ${S}_{s}= 0.000002\; $$ {\mathrm{m}}^{-1}$, $ b=30\;\mathrm{m} $, $ {h}_{0}=36\;\mathrm{m} $ and $ r=10\;\mathrm{m} $ in semi-log scales.
Figure 5. Time-R value curves for different
$ {S}_{s} $ valueNotes: With $ Q=0.04\;{\mathrm{m}}^{3}/\mathrm{s} $, ${K}_{r}=0.00000348\;\mathrm{m}/\mathrm{s}$, $ {S}_{y}=0.3 $, $ b= $$ 30\;\mathrm{m} $, $ {h}_{0}=36\;\mathrm{m} $, $ n=1.4 $ and $ r=10\;\mathrm{m} $ in semi-log scales
Figure 6. Time-Drawdown curves for different
$ {S}_{s} $ valueNotes: With $Q=0.04\;{\mathrm{m}}^{3}/\mathrm{s}$, ${K}_{r}=0.00000348\;\mathrm{m}/\mathrm{s}$, $ {S}_{y}= 0.3 $, b = 30 m, $ {h}_{0}=36\;\mathrm{m} $, $ n=1.4 $ and $ r=10\;\mathrm{m} $ in semi-log scales
Figure 7. a)
$ R $ -time curves and b) time-drawdown curves for different$ {K}_{r} $ valueNotes: With $ Q=0.04\;{\mathrm{m}}^{3}/\mathrm{s} $, $ {S}_{y}=0.3 $, $ {S}_{s}=0.000002\;{\mathrm{m}}^{-1} $, b = 30 m, $ {h}_{0}=36\;\mathrm{m} $, $ n=1.4 $ and $ r=10\;\mathrm{m} $ in semi-log scales
Figure 8. Sensitivity analysis of aquifer parameters
Notes: With $ Q=0.04\;{\mathrm{m}}^{3}/\mathrm{s} $, ${S}_{s}=0.000002\;{\mathrm{m}}^{-1}$, $ {S}_{y}=0.3 $, b=30 m, $ {h}_{0}=36\;\mathrm{m} $, $ r=10\;\mathrm{m} $, $ n=1.4 $ and ${K}_{r}= 0.000003475\;\mathrm{m}/\mathrm{s}$ in semi-log scales
-
Basak P. 1976. Steady non-Darcian seepage through embankments. Journal of the Irrigation and Drainage Division, 102(4): 435−443. DOI: 10.1061/JRCEA4.0001256. Bordier C, Zimmer D. 2000. Drainage equations and non-Darcian modeling in coarse porous media or geosynthetic materials. Journal of Hydrology, 228: 174−187. DOI: 10.1016/S0022-1694(00)00151-7. Chen CX, Hu LT, Wang XS. 2006. Analysis of stead ground water flow toward wells in a confined-unconfined aquifer. Ground Water, 44(4): 609−612. DOI: 10.1111/j.1745-6584.2006.00170.x. Chen CX, Wan JW, Zhan HB. 2003. Theoretical and experimental studies of coupled seepage-pipe flow to a horizontal well. Journal of Hydrology, 281(1-2): 159−171. DOI: 10.1016/S0022-1694(03)00207-5. Elango K, Swaminathan K. 1980. A finite-element model for concurrent confined-unconfined zones in an aquifer. Journal of Hydrology, 46(3-4): 289−299. DOI: 10.1016/0022-1694(80)90082-7. El-Hames AS. 2020. Development of a simple method for determining the influence radius of a pumping well in steady-state condition. Journal of Groundwater Science and Engineering, 8(2): 11. DOI: 10.19637/j.cnki.2305-7068.2020.02.001. Feng Q, Wen Z. 2016. Non-Darcian flow to a partially penetrating well in a confined aquifer with a finite-thickness skin. Hydrogeology Journal, 24(5): 1287−1296. DOI: 10.1007/s10040-016-1389-8. Hao HB, Lv J, Chen YM, et al. 2021. Research advances in non-Darcian flow in low permeability media. Journal of Groundwater Science and Engineering, 9(1): 83−92. DOI: 10.19637/j.cnki.2305-7068.2021.01.008. Houben GJ. 2015. Review: Hydraulics of water wells-flow laws and influence of geometry. Hydrogeology Journal, 23(8): 1633−1657. DOI: 10.1007/s10040-015-1312-8. Hu LT, Chen CX. 2008. Analytical methods for transient flow to a well in a confined-unconfined aquifer. Ground water, 46(4): 642−646. DOI: 10.1111/j.1745-6584.2008.00436.x. Huang YC, Yeh HD. 2007. The use of sensitivity analysis in on-line aquifer parameter estimation. Journal of Hydrology, 335(3-4): 406−418. DOI: 10.1016/j.jhydrol.2006.12.007. Ji SH, Koh YK. 2015. Nonlinear groundwater flow during a slug test in fractured rock. Journal of Hydrology, 520: 30−36. DOI: 10.1016/j.jhydrol.2014.11.039. Li J, Xia XH, Zhan H, et al. 2021. Non-Darcian flow for an artificial recharge well in a confined aquifer with clogging-related permeability reduction. Advances in Water Resources, 147(8): 103820. DOI: 10.1016/j.advwatres.2020.103820. Liu MM, Chen YF, Zhan HB, et al. 2017. A generalized Forchheimer radial flow model for constant-rate tests. Advances in Water Resources, 107(sep.): 317−325. DOI: 10.1016/j.advwatres.2017.07.004. Marsily GD. 1986. Quantitative hydrogeology. Fontainebleau, France: Pairs School of Mines. Mathias SA, Wen Z. 2015. Numerical simulation of Forchheimer flow to a partially penetrating well with a mixed-type boundary condition. Journal of Hydrology, 524: 53−61. DOI: 10.1016/j.jhydrol.2015.02.015. Mathias SA, Moutsopoulos KN. 2016. Approximate solutions for Forchheimer flow during water injection and water production in an unconfined aquifer. Journal of Hydrology, 538: 13−21. DOI: 10.1016/j.jhydrol.2016.03.048. Mawlood D, Mustafa J. 2016. Comparison between Neuman (1975) and Jacob (1946) application for analysing pumping test data of unconfined aquifer. Journal of Groundwater Science and Engineering, 4(3): 165−173. DOI: 10.21271/zjpas.32.2.2. Moench AF, Prickett TA. 1972. Radial flow in an infinite aquifer undergoing conversion from artesian to water table conditions. Water Resource Research, 8(2): 494−499. DOI: 10.1029/WR008i002p00494. Moench AF, Garabedian SP, LeBlanc DR. 2001. Estimation of hydraulic parameters from an unconfined aquifer test conducted in a glacial outwash deposit, Cape Cod, Massachusetts. US Geology Survey Professional Paper, (1629): 140. Moutsopoulos KN, Tsihrintzis VA. 2005. Approximate analytical solutions of the Forchheimer equation. Journal of Hydrology, 309(1-4): 93−103. DOI: 10.1016/j.jhydrol.2004.11.014. Moutsopoulos KN. 2007. One-dimensional unsteady inertial flow in phreatic aquifers, induced by a sudden change of the boundary head. Transport Porous Media, 70(1): 97−125. DOI: 10.1007/s11242-006-9086-z. Moutsopoulos KN. 2009. Exact and approximate analytical solutions for unsteady fully developed turbulent flow in porous media and fractures for time dependent boundary conditions. Journal of Hydrology, 369(1-2): 78−89. DOI: 10.1016/j.jhydrol.2009.02.025. Qian JZ, Zhan HB, Zhao WD. 2005. Experimental study of turbulent unconfined groundwater flow in a single fracture. Journal of Hydrology, 311(1-4): 134−142. DOI: 10.1016/j.jhydrol.2005.01.013. Sen Z. 1987. Non-Darcian flow in fractured rocks with a linear flow pattern. Journal of Hydrology, 92(1-2): 43−57. DOI: 10.1016/0022-1694(87)90088-6. Sen Z. 1989. Non-linear flow toward wells. Journal of Hydrology Engineering, 115(2): 193−209. DOI: 10.1061/(ASCE)0733-9429(1989)115:2(193). Sen Z. 1990. Nonliear radical flow in confined aquifers toward large-dsameter wells. Water Resource Research, 26(5): 1103−1109. DOI: 10.1016/0148-9062(90)91166-5. Soni JP, Islam N, Basak P. 1978. An experimental evaluation of non-Darcian flow in porous media. Jounal of Hydrology, 38(3-4): 231−241. DOI: 10.1016/0022-1694(78)90070-7. Wang QR, Zhan HB, Wang YX. 2015. Non-Darcian effect on slug test in a leaky confined aquifer. Journal of Hydrology, 527: 747−753. DOI: 10.1016/j.jhydrol.2015.05.038. Wang XF. 2011. Fundamentals of hydrogeology. Hydrogeology & Engineering Geology, 38 (03): 1. (in Chinese) Wang XS, Wan L, Hu B. 2009. New approximate solutions of horizontal confined–unconfined flow. Journal of Hydrology (Amsterdam), 376(3-4): 417−427. DOI: 10.1016/j.jhydrol.2009.07.050. Wen Z, Huang GH, Zhan HB. 2006. Non-Darcian flow in a single confined vertical fracture toward a well. Journal of Hydrology, 330(3): 698−708. DOI: 10.1016/j.jhydrol.2006.05.001. Wen Z, Huang GH. Zhan HB. 2008a. Non-Darcian flow to a well in an aquifer–aquitard system. Advances in Water Resources, 31(12): 1754−1763. DOI: 10.1016/j.advwatres.2008.09.002. Wen Z, Huang GH, Zhan HB. 2008b. Two-region non-Darcian flow toward a well in a confined aquifer. Advances in Water Resources, 31(5): 818−827. DOI: 10.1016/j.advwatres.2008.01.014. Wen Z, Huang GH, Zhan HB. 2008c. An analytical solution for non-Darcian flow in a confined aquifer using the power law function. Advances in Water Resources, 31(1): 44−55. DOI: 10.1016/j.advwatres.2007.06.002. Wen Z, Huang GH, Zhan HB. 2009. A numerical solution for non-Darcian flow to a well in a confined aquifer using the power law function. Journal of Hydrology, 364(1/2): 99−106. DOI: 10.1016/j.jhydrol.2008.10.009. Wen Z, Huang GH, Zhan HB. 2011. Non-Darcian flow to a well in a leaky aquifer using the Forchheimer equation. Hydrogeology Journal, 19(3): 563−572. DOI: 10.1007/s10040-011-0709-2. Wen Z, Wang QR. 2013. Approximate analytical and numerical solutions for radial non-Darcian flow to a well in a leaky aquifer with wellbore storage and skin effect. International Journal for Numerical & Analytical Methods in Geomechanics, 37(11): 1453−1469. DOI: 10.1002/nag.2091. Wen Z, Liu K, Chen XL. 2013. Approximate analytical solution for non-Darcian flow toward a partially penetrating well in a confined aquifer. Journal of Hydrology, 498: 124−131. DOI: 10.1016/j.jhydrol.2013.06.027. Wu YS. 2001. Non-Darcy displacement of immiscible fluids in porous media. Water Resource Research, 37(12): 2943−2950. DOI: 10.1029/2001WR000389. Wu YS. 2002a. An approximate analytical solution for non-Darcy flow toward a well in fractured media. Water Resource Research, 38(3): 5−1. DOI: 10.1029/2001WR000713. Wu YS. 2002b. Numerical simulation of single-phase and multi-phase non-Darcy flow in porous and fractured reservoirs. Transport Porous Media, 49(2): 209−240. DOI: 10.1023/A:1016018020180. Xiao L, Guo GH, Chen LH, et al. 2022. Theory of transient confined-unconfined flow in a confined aquifer considering delayed responses of water table. Journal of Hydrology, 2022(608): 127644. DOI: 10.1016/j.jhydrol.2022.127644. Xiao L, Liu JJ, Gan FW, et al. 2023. A semi-analytical solution for transient confined–unconfined flow with non-Darcian effect. Journal of Hydrologic Engineering, 28(5): 04023012. DOI: 10.1061/JHYEFF.HEENG-5845. Xiao L, Ye M, Xu YX. 2018. A new solution for confined-unconfined flow toward a fully penetrating well in a confined aquifer. Groundwater, 56(6): 959−968. DOI: 10.1111/gwat.12642. Zhao RJ, Mao DQ, Liu ZB, et al. 2021. An analysis of sequential water releasing tests of the confined aquifers in a coal mine based on hydraulic tomography. Hydrogeology & Engineering Geology, 48(1): 1−9. (in Chinese) DOI: 10.16030/j.cnki.issn.1000-3665.202003024. Zong YJ, Chen LH, Liu JJ, et al. 2022. Analytical solutions for constant-rate test in bounded confined aquifers with non-Darcian effect. Journal of Groundwater Science and Engineering, 10(4): 311−321. DOI: 10.19637/j.cnki.2305-7068.2022.04.001. -
下载:
点击查看大图
计量
- 文章访问数: 881
- HTML全文浏览量: 373
- PDF下载量: 131
- 被引次数: 0
