E-mail alert
Rss
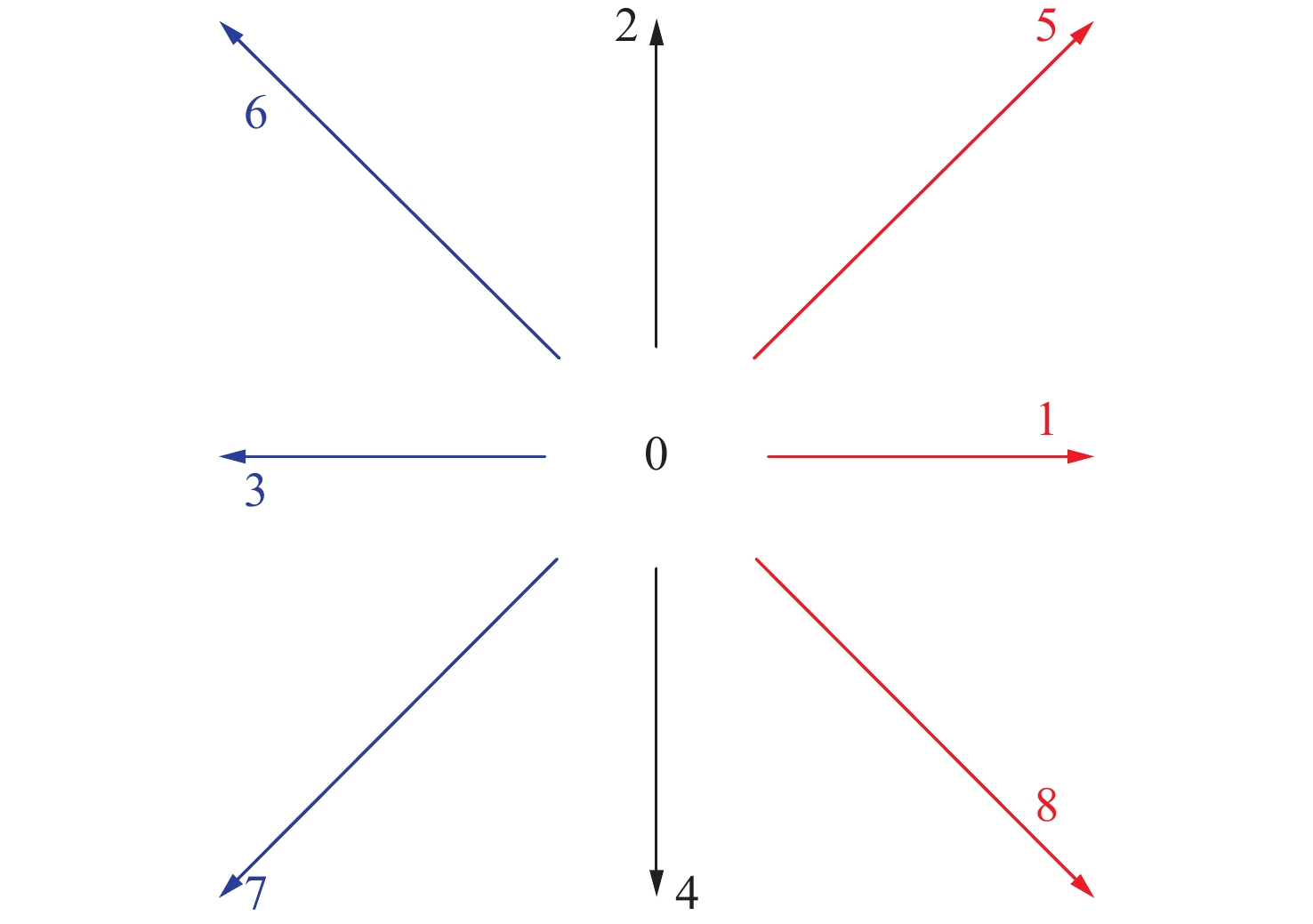
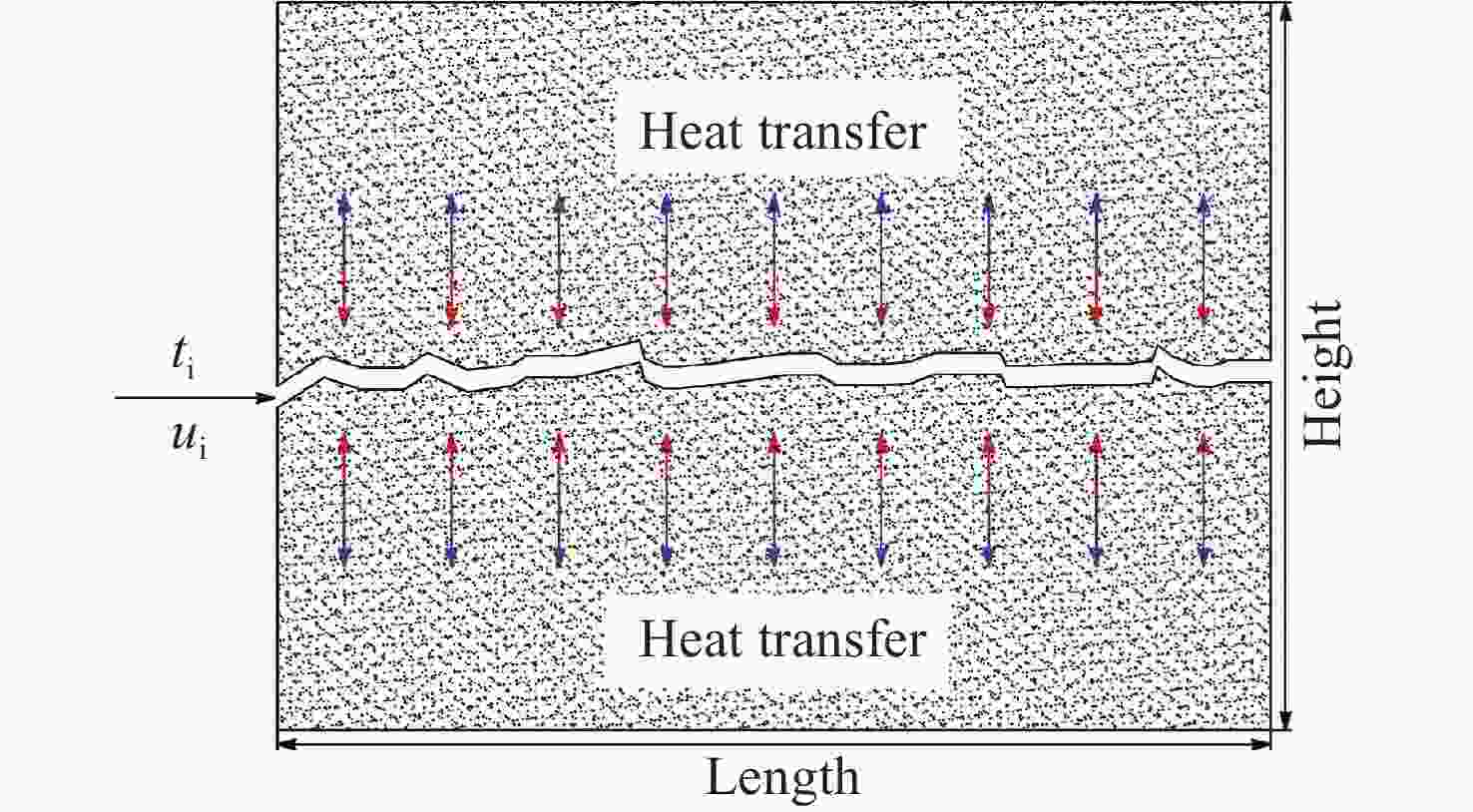
A combined method using Lattice Boltzmann Method (LBM) and Finite Volume Method (FVM) to simulate geothermal reservoirs in Enhanced Geothermal System (EGS)
-
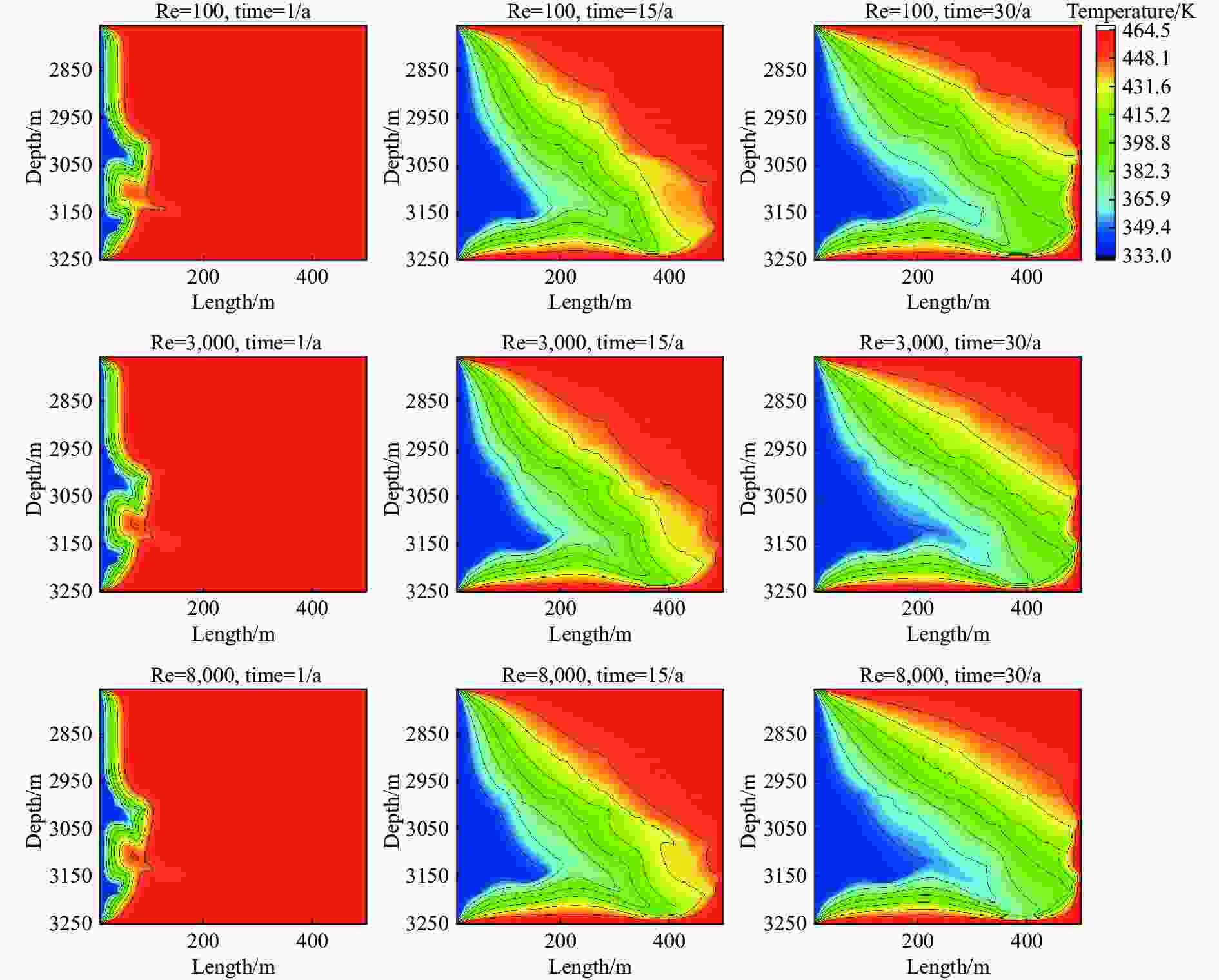
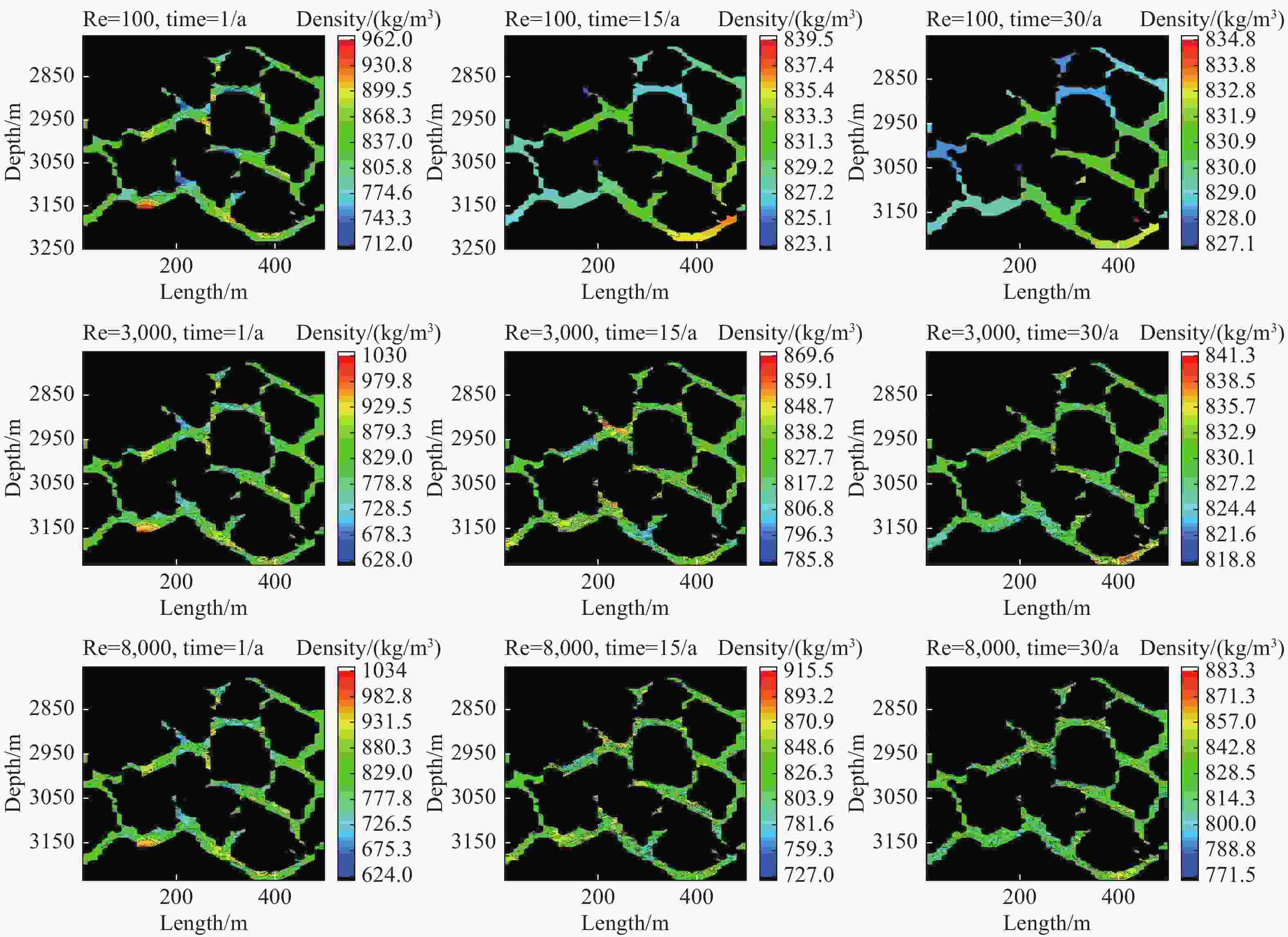
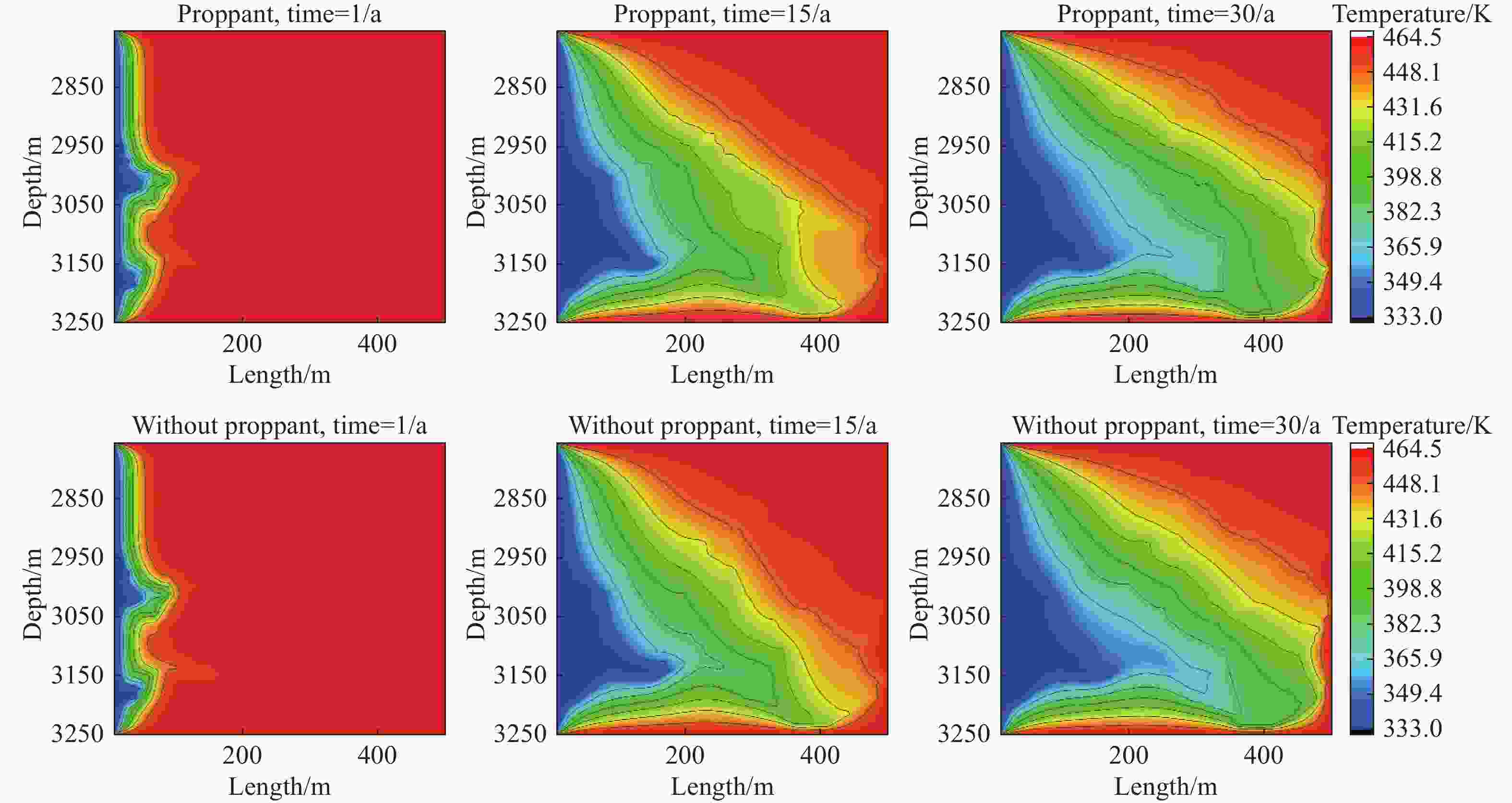
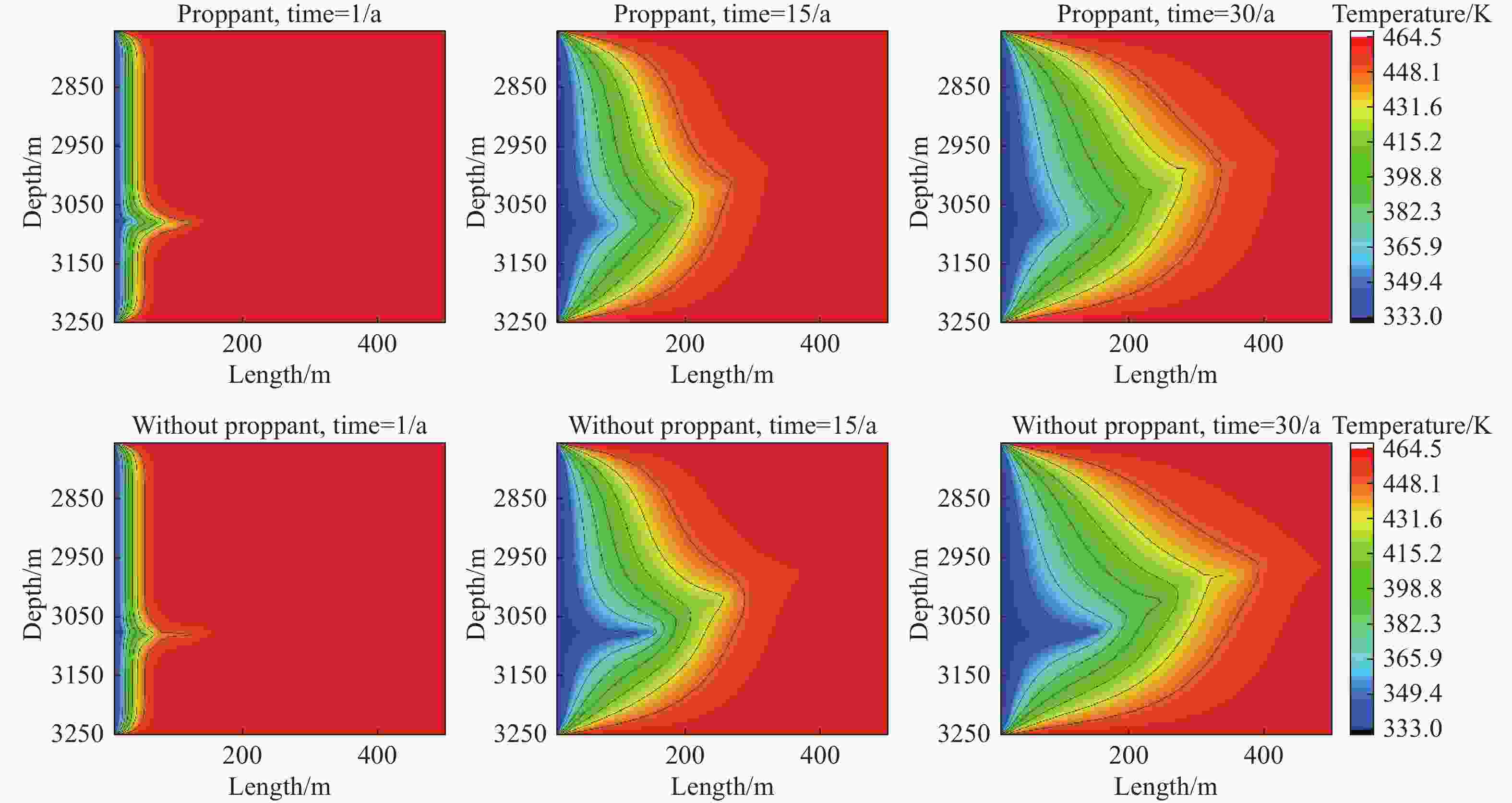
Abstract: With the development of industrial activities, global warming has accelerated due to excessive emission of CO2. Enhanced Geothermal System (EGS) utilizes deep geothermal heat for power generation. Although porous medium theory is commonly employed to model geothermal reservoirs in EGS, Hot Dry Rock (HDR) presents a challenge as it consists of impermeable granite with zero porosity, potentially distorting the physical interpretation. To address this, the Lattice Boltzmann Method (LBM) is employed to simulate CO2 flow within geothermal reservoirs and the Finite Volume Method (FVM) to solve the energy conservation equation for temperature distribution. This combined method of LBM and FVM is implemented using MATLAB. The results showed that the Reynolds numbers (Re) of 3,000 and 8,000 lead to higher heat extraction rates from geothermal reservoirs. However, higher Re values may accelerate thermal breakthrough, posing challenges to EGS operation. Meanwhile, non-equilibrium of density in fractures becomes more pronounced during the system's life cycle, with non-Darcy's law becoming significant at Re values of 3,000 and 8,000. Density stratification due to buoyancy effects significantly impacts temperature distribution within geothermal reservoirs, with buoyancy effects at Re=100 under gravitational influence being noteworthy. Larger Re values (3,000 and 8,000) induce stronger forced convection, leading to more uniform density distribution. The addition of proppant negatively affects heat transfer performance in geothermal reservoirs, especially in single fractures. Practical engineering considerations should determine the quantity of proppant through detailed numerical simulations.
-
Figure 3. Variation of Criterion with the grids number of 50×100, 100×200, 150×300, 200×400 and 250×500
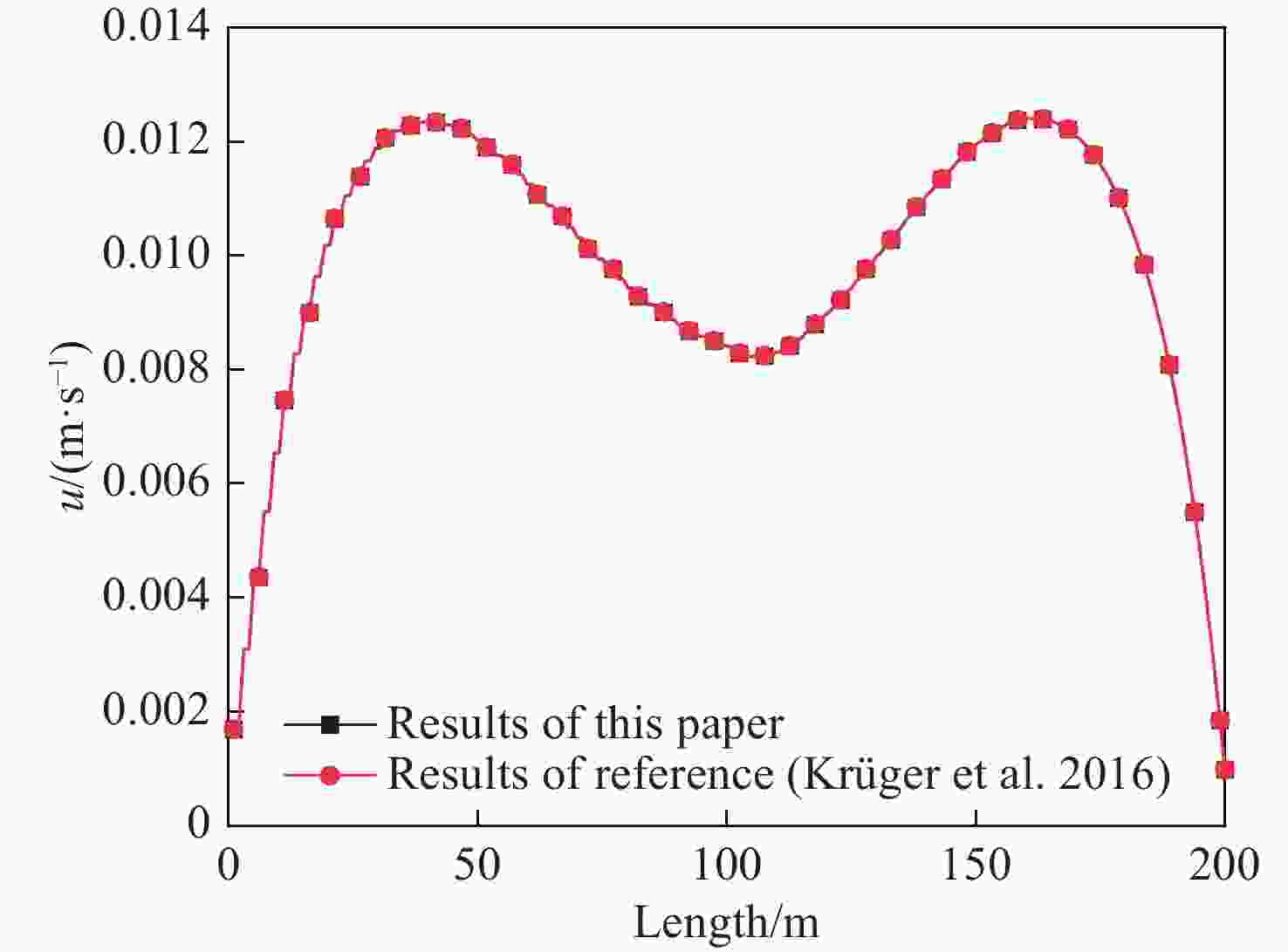
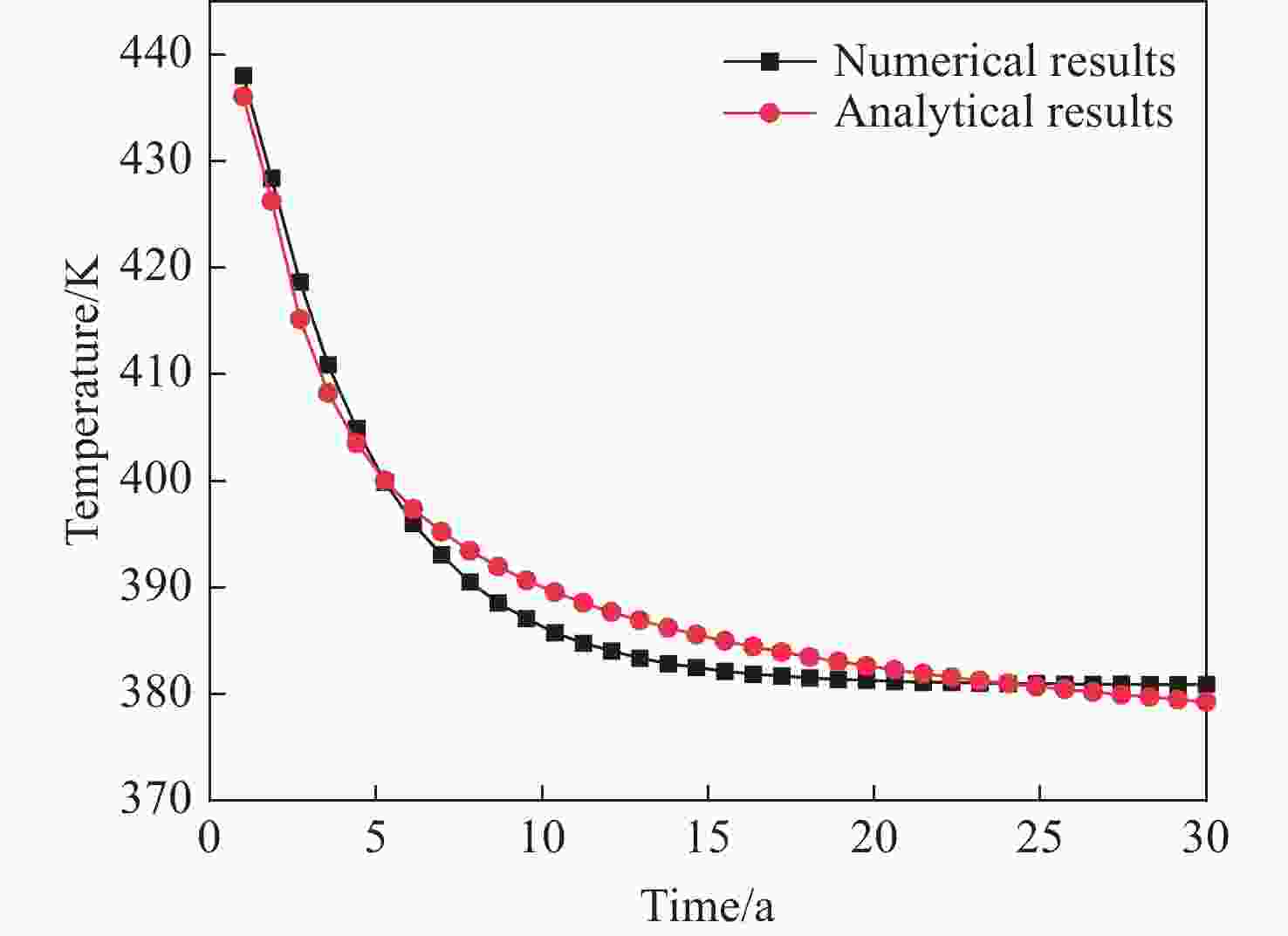
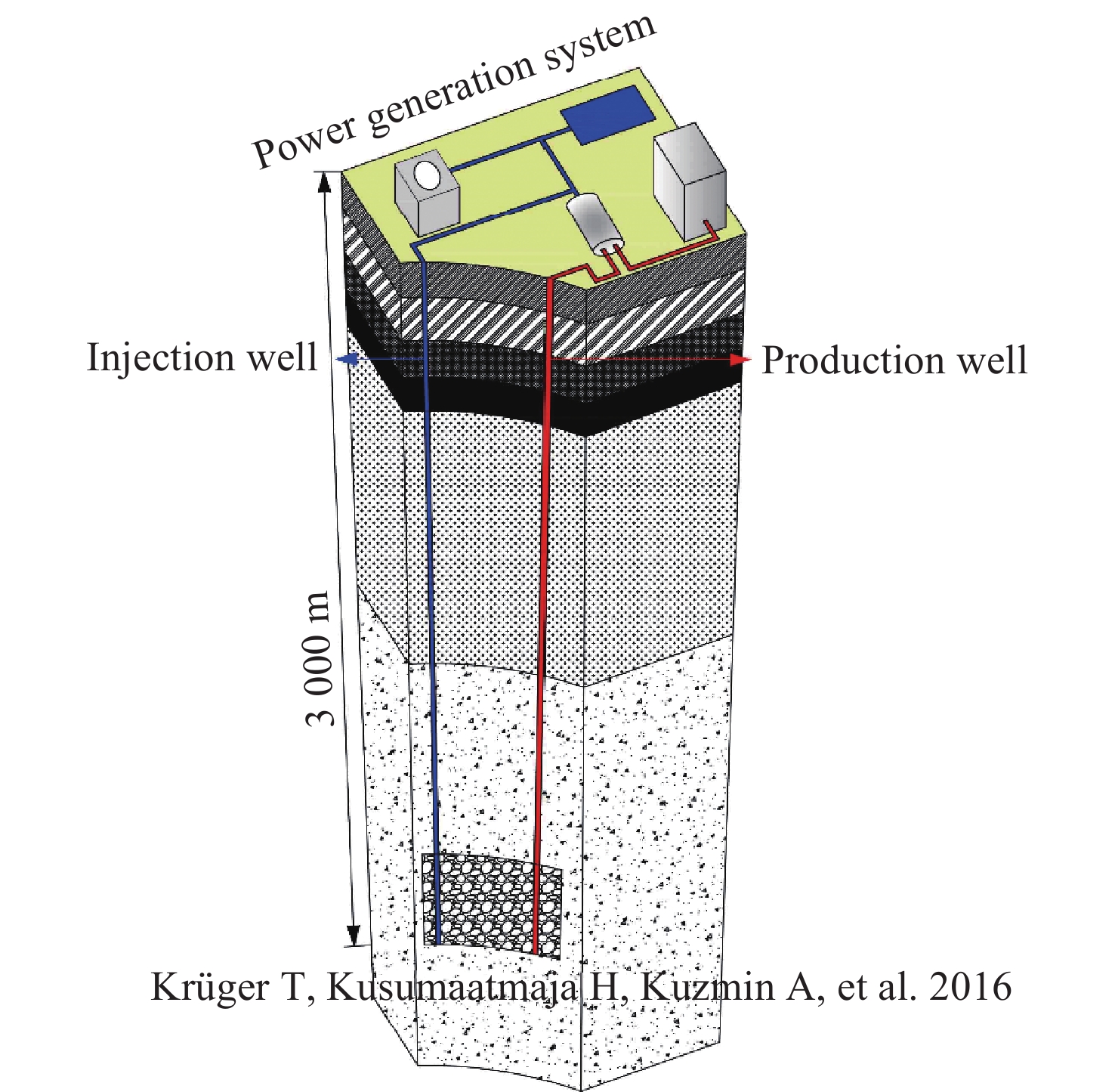
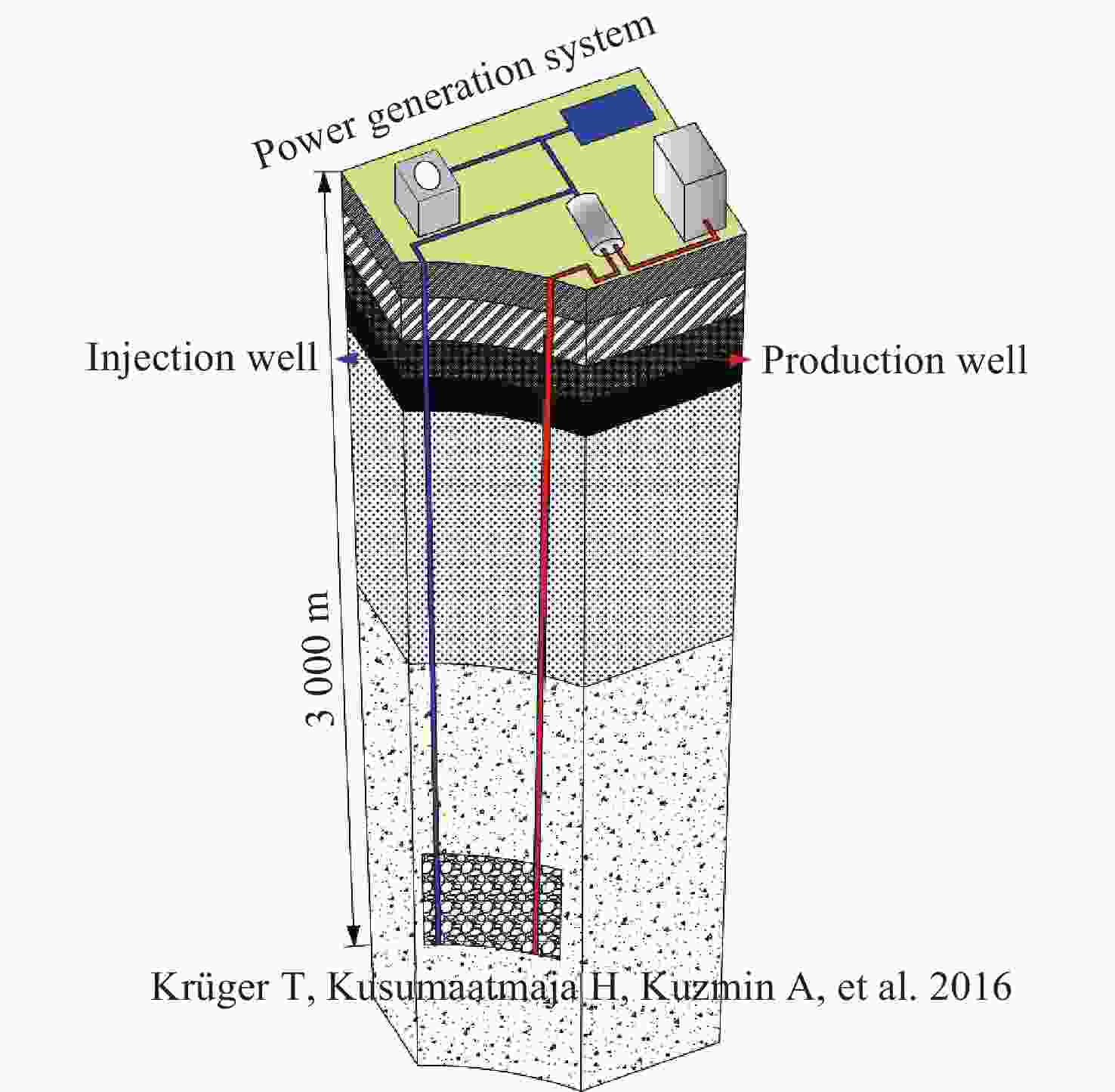
Figure 4. Comparison between the results of reference (Krüger et al. 2016) and this paper based on the velocity distribution along the centerline for a lid-driven cavity
Figure 6. Comparison between the numerical results and analytical results in a single fracture
Figure 7. Scale of the region in geothermal reservoir for complex fracture distributions, single fracture, complex fracture distributions with proppant and single fracture with proppant
Figure 16. Temperature distribution in the fractured reservoir with single fracture during 30 years
Table 1. Initial and boundary conditions for base simulation case
Parameters Value Unit Mass flow rate 20 kg/s Rock thermal conductivity 3.0 W/(m·K) Rock density 2,623 kg/m3 Specific thermal capacity of rock 980 J/(kg·K) Initial temperature of rock 441.82 K Computing time 30 a Inlet temperature of the single fracture 343.15 K Fracture aperture 0.0001 m External diameter 0.137 m Inside diameter 0.124 m Thermal conductivity of wellbore wall 0.52 W/(m·K) Elastic modulus of rock 40 GPa Poisson's ratio of rock 0.2 Pressure at 3,000 m subsurface 30 MPa Injection concentration 0.018 mol/kg Ambient temperature 293.15 K Size of fractured reservoir 500 × 500 × 500 m3 
下载: 导出CSV
Table 2. Initial and boundary conditions in this section (Zhong et al. 2022)
Properties Value Unit Properties Value Unit Density of HDR 2,623 kg/m3 Normal stress on the top boundary 20 MPa Specific heat capacity of HDR 980 J/(kg·K) Normal stress on the bottom boundary 30 MPa Thermal conductivity of HDR 3 W/(m·K) Normal stress on the two sides 20 MPa Porosity in fracture system 0.5 - Rock Young's modulus 24 GPa Porosity in matrix 1 × 10−5 - Rock Possion's ratio 0.15 Permeability in fracture system 1 × 10−13 m2 Thermal expansion coefficient 2×10−6 1/K Permeability in matrix 9 × 10−19 m2 Biot coefficient 0.79 Runtime 30 years Mass flow rate 45 kg/s
下载: 导出CSV
-
Al Balushi F, Zhang Q, Dahi Taleghani A. 2023. Improving enhanced geothermal systems performance using adaptive fracture conductivity. Applied Thermal Engineering, 233: 121206. DOI: 10.1016/j.applthermaleng.2023.121206. Avanthi Isaka BL, Ranjith PG, Rathnaweera TD. 2019. The use of super-critical carbon dioxide as the working fluid in enhanced geothermal systems (EGSs): A review study. Sustainable Energy Technologies and Assessments, 36: 100547. DOI: 10.1016/j.seta.2019.100547. Babamahmoudi S, Saeedi Dehaghani AH, Hosseini Moghadam A. 2023. Absolute permeability assessment of porous structures under different boundary conditions using lattice Boltzmann method. Geoenergy Science and Engineering, 221: 211357. DOI: 10.1016/j.geoen.2022.211357. Cheng Q, Wang X, Ghassemi A. 2019. Numerical simulation of reservoir stimulation with reference to the Newberry EGS. Geothermics, 77: 327−343. DOI: 10.1016/j.geothermics.2018.09.011. Ding Q, Huang J, Chen J, et al. 2024. Climate warming, renewable energy consumption and rare earth market: Evidence from the United States. Energy, 290: 130276. DOI: 10.1016/j.energy.2024.130276. Dokmak H, Faraj K, Faraj J, et al. 2024. Geothermal systems classification, coupling, and hybridization: A recent comprehensive review. Energy and Built Environment, 1-20. Ghassemi A, Nygren A, Cheng A. 2008. Effects of heat extraction on fracture aperture: A poro–thermoelastic analysis. Geothermics, 37: 525−539. DOI: 10.1016/j.geothermics.2008.06.001. Guo Z, Zheng C, Shi B. 2002. An extrapolation method for boundary conditions in lattice Boltzmann method. Physics of Fluids, 14: 2007−2010. DOI: 10.1063/1.1471914. He X, Zou Q, Luo LS, et al. 1997. Analytic solutions of simple flows and analysis of nonslip boundary conditions for the Lattice Boltzmann BGK model. Journal of Statistical Physics, 87: 115−136. DOI: 10.1007/BF02181482. Hu Z, Xu T, Moore J, et al. 2022. Investigation of the effect of different injection schemes on fracture network patterns in hot dry rocks - A numerical case study of the FORGE EGS site in Utah. Journal of Natural Gas Science and Engineering, 97: 104346. DOI: 10.1016/j.jngse.2021.104346. Jiao K, Han D, Li J, et al. 2021. A novel LBM-DEM based pore-scale thermal-hydro-mechanical model for the fracture propagation process. Computer and Geotechnics, 139: 104418. DOI: 10.1016/j.compgeo.2021.104418. Krüger T, Kusumaatmaja H, Kuzmin A, et al. 2016. The Lattice Boltzmann Method-Principles and practice. Springer International Publish. Li S, Wang S, Tang H. 2022. Stimulation mechanism and design of enhanced geothermal systems: A comprehensive review. Renewable and Sustainable Energy Reviews, 155: 111914. DOI: 10.1016/j.rser.2021.111914. Li T, Han D, Yang F, et al. 2021. Modeling study of the thermal-hydraulic-mechanical coupling process for EGS based on the framework of EDFM and XFEM. Geothermics, 89: 101953. DOI: 10.1016/j.geothermics.2020.101953. Liao J, Hu K, Mehmood F, et al. 2023. Embedded discrete fracture network method for numerical estimation of long-term performance of CO2-EGS under THM coupled framework. Energy, 285: 128734. DOI: 10.1016/j.energy.2023.128734. Luo Z, Wu Y, Zhou L, et al. 2021. Trade-off between vegetation CO2 sequestration and fossil fuel-related CO2 emissions: A case study of the Guangdong–Hong Kong–Macao Greater Bay area of China. Sustain Cities and Society, 74: 103195. DOI: 10.1016/j.scs.2021.103195. Moradi I, D'Orazio A. 2023. Lattice Boltzmann Method Pore-scale simulation of fluid flow and heat transfer in porous media: Effect of size and arrangement of obstacles into a channel. Engineering Analysis with Boundary Elements, 152: 83−103. DOI: 10.1016/j.enganabound.2023.04.007. Mukuhira Y, Ito T, Asanuma H, et al. 2020. Evaluation of flow paths during stimulation in an EGS reservoir using microseismic information. Geothermics, 87: 101843. DOI: 10.1016/j.geothermics.2020.101843. Olasolo P, Juárez MC, Morale MP, et al. 2016. Enhanced geothermal systems (EGS): A review. Renewable and Sustainable Energy Reviews, 56: 133−144. DOI: 10.1016/j.rser.2015.11.031. Rohit RV, Kiplangat DC, Veena R, et al. 2023. Tracing the evolution and charting the future of geothermal energy research and development. Renewable and Sustainable Energy Reviews, 184: 113531. DOI: 10.1016/j.rser.2023.113531. Sun R, Shen J, Grasby SE, et al. 2022. CO2 buildup drove global warming, the Marinoan deglaciation, and the genesis of the Ediacaran cap carbonates. Precambrian Research, 383: 106891. DOI: 10.1016/j.precamres.2022.106891. Sun ZX, Zhang X, Xu Y, et al. 2017. Numerical simulation of the heat extraction in EGS with thermal-hydraulic-mechanical coupling method based on discrete fractures model. Energy, 120: 20−33. DOI: 10.1016/j.energy.2016.10.046. Qian YH, D'Humières D, Lallemand P. 1992. Lattice BGK Models for Navier-Stokes Equation. Europhys Lett, 17: 479. DOI: 10.1209/0295-5075/17/6/001. Yao J, Zhang X, Sun Z, et al. 2018. Numerical simulation of the heat extraction in 3D-EGS with thermal-hydraulic-mechanical coupling method based on discrete fractures model. Geothermics, 74: 19−34. DOI: 10.1016/j.geothermics.2017.12.005. Zhang EY, Wen DG, Wang GL, et al. 2022. The first power generation test of hot dry rock resources exploration and production demonstration project in the Gonghe Basin, Qinghai Province, China. China Geology, 5(3): 372−382. DOI: 10.31035/cg2022038. Zhang W, Han D, Wang B, et al. 2023. Thermal-hydraulic-mechanical-chemical modeling and simulation of an enhanced geothermal system based on the framework of extended finite element methods - Embedded discrete fracture model. Journal of Cleaner Production, 415: 137630. DOI: 10.1016/j.jclepro.2023.137630. Zhong C, Xu T, Yuan Y, et al. 2022. The feasibility of clean power generation from a novel dual-vertical-well enhanced geothermal system (EGS): A case study in the Gonghe Basin, China. Journal of Cleaner Production, 344: 131109. DOI: 10.1016/j.jclepro.2022.131109. Zhou D, Tatomir A, Niemi A, et al. 2022. Study on the influence of randomly distributed fracture aperture in a fracture network on heat production from an enhanced geothermal system (EGS). Energy, 250: 123781. DOI: 10.1016/j.energy.2022.123781. Zou Q, He X. 1997. On pressure and velocity boundary conditions for the lattice Boltzmann BGK model. Physics of Fluids, 9: 1591−1598. DOI: 10.1063/1.869307. -
点击查看大图
图(16) / 表ll (2)
计量
- 文章访问数: 176
- HTML全文浏览量: 94
- PDF下载量: 102
- 被引次数: 0
