E-mail alert
Rss
Web-based tool for analyzing the seawater-freshwater interface using analytical solutions and SEAWAT code comparison
-
Abstract: Saltwater Intrusion (SI) poses a significant environmental threat to freshwater resources in coastal aquifers globally. The primary objective of this research is to illustrate the variations in the saltwater-freshwater interface using several established analytical solutions, integrated within a user-friendly web-based tool. Three case studies, including a hypothetical unconfined coastal aquifer, an experimental coastal aquifer, and a real-world coastal aquifer in Gaza, were applied to examine the interface dynamics using the developed tool, built with JavaScript. To simulate variable-density flow within the Gaza coastal aquifer, the public domain code SEAWAT was employed. The resulting lengths of seawater intrusion, as simulated by SEAWAT and the observed toe length, were compared with those obtained from the web-based analytical solutions under both constant head and constant flux boundary conditions. This comparison demonstrated a strong correlation between the experimental results, SEAWAT model outputs, and analytical solutions. This research provides valuable insights into SI in coastal aquifers, with a specific focus on the impact of Sea Level Rise (SLR) on the shifting position of the seawater intrusion toe. The outcomes are presented through an accessible web-based interface, thereby promoting broader dissemination and practical application of the research outcomes.
-
Key words:
- Saltwater Intrusion /
- Numerical Simulation /
- Coastal Aquifers /
- Sea Level Rise /
- SEAWAT
-
Figure 1. Saltwater intrusion wedge evolution over time (15, 30, 45, 60, 75, and 95 minutes) after increasing the freshwater head to 31.40 cm
Figure 3. Input parameters for calculating the seawater-freshwater interface for the hypothetical coastal aquifer using the analytical solutions Gyhben Herzberg, Glover, Rumer-Herleman, and Verruijt
Figure 4. Seawater-freshwater interface for a hypothetical coastal aquifer based on the analytical solutions of: (a) Gyhben Herzberg, (b) Glover, (c) Rumer-Herleman, and (d) Verruijt
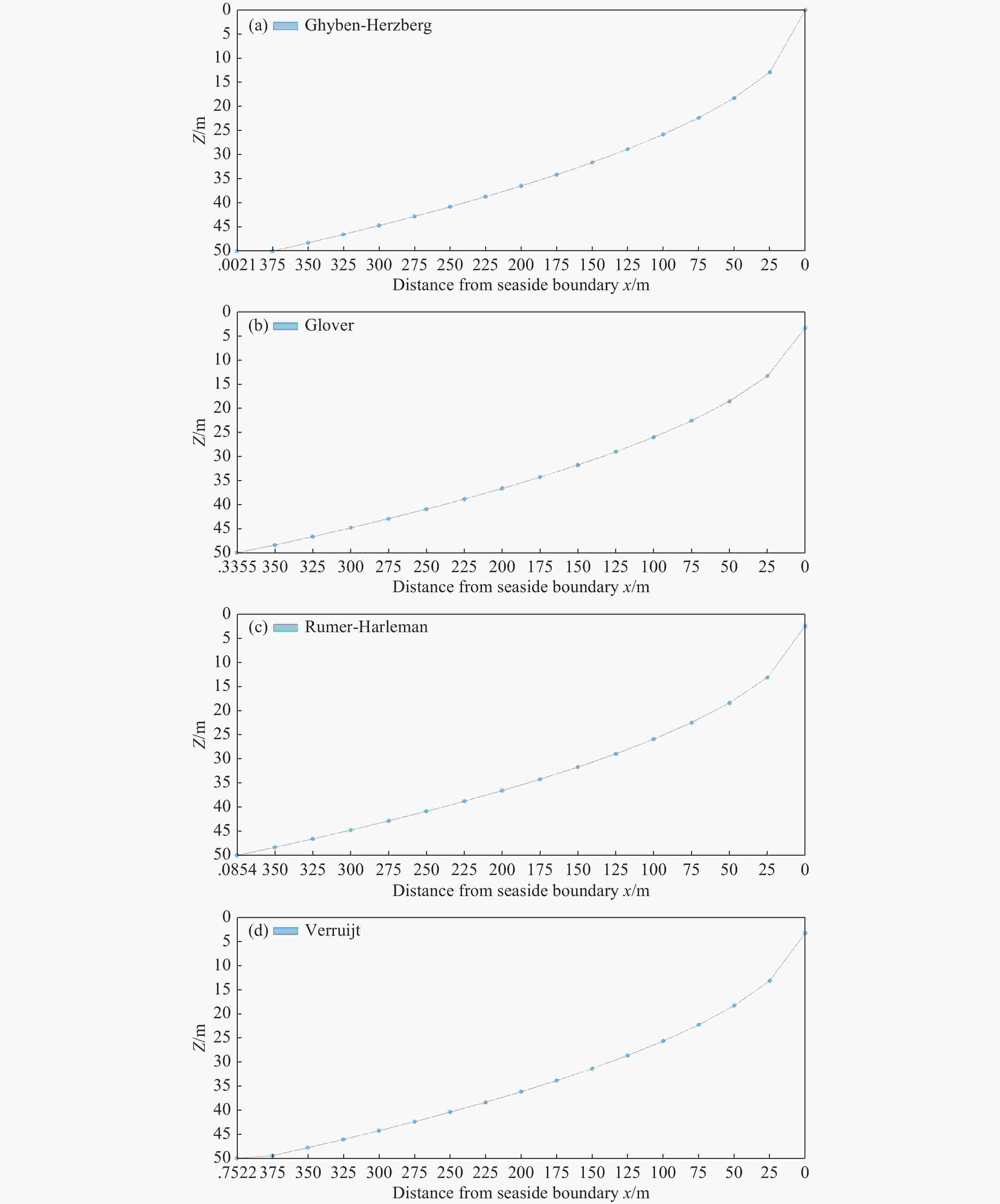
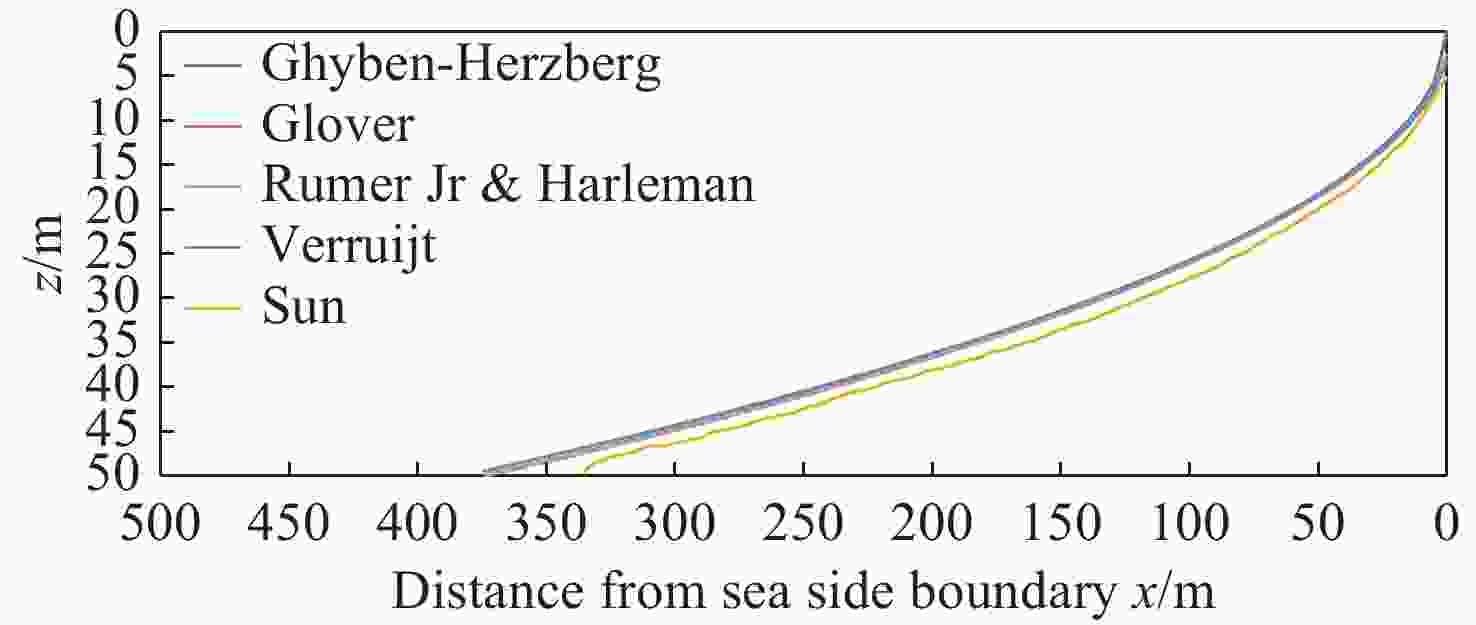
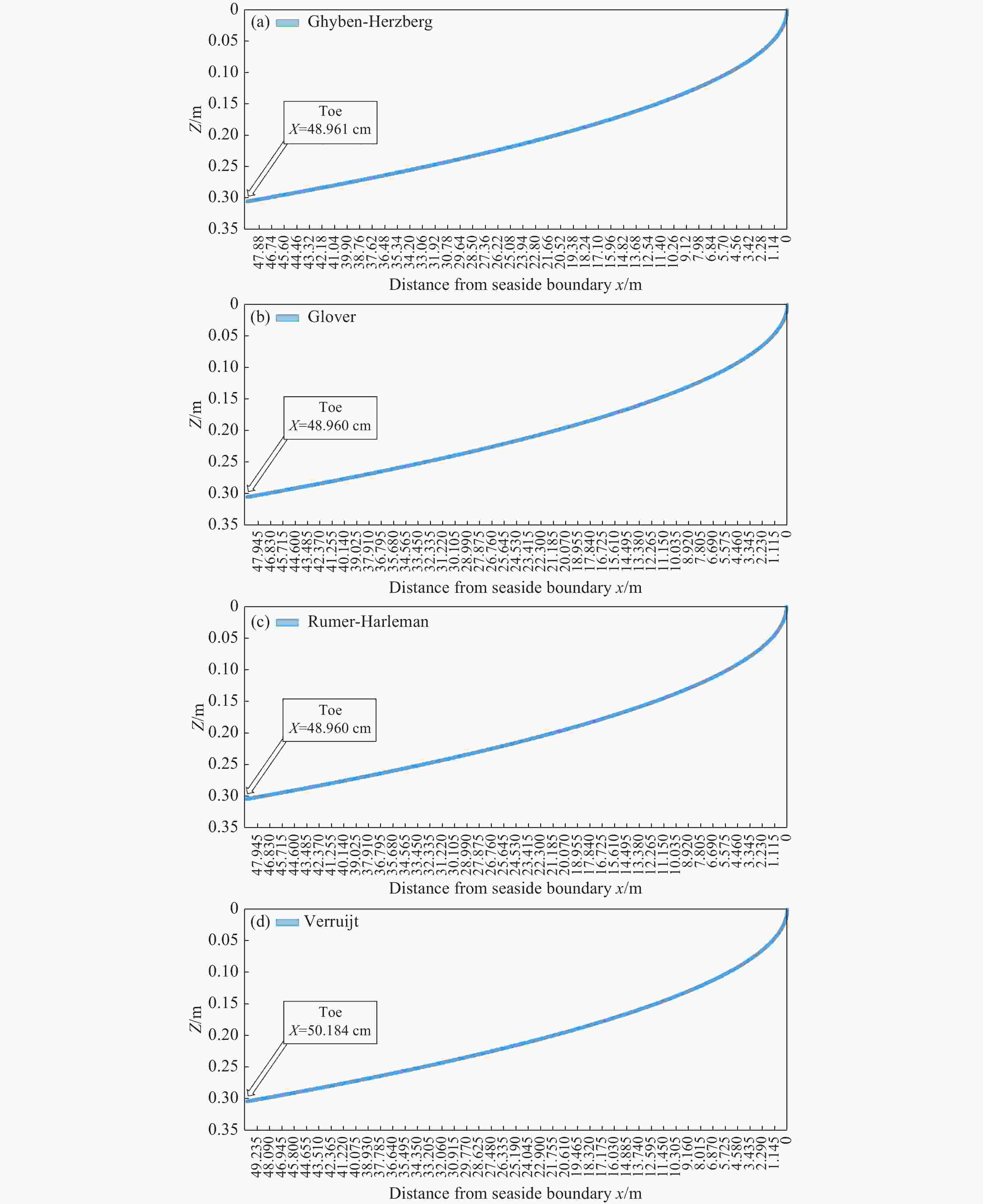
Figure 5. Comparison between the simulated SW-FW interface for the hypothetical unconfined coastal aquifer (from Sun et al. 2021) and the analytical solutions of Gyhben-Herzberg, Glover, Rumer-Herleman, and Verruijt through the web-based interface model
Figure 6. Input Parameters for calculating the seawater-freshwater interface using the analytical solutions of Gyhben-Herzberg, Glover, Rumer-Herleman, and Verruijt for the experimental coastal aquifer
Figure 7. Seawater-freshwater interface for the experimental coastal aquifer based on the analytical solutions of: (a) Gyhben-Herzberg, (b) Glover, (c) Rumer-Herleman, and (d) Verruijt
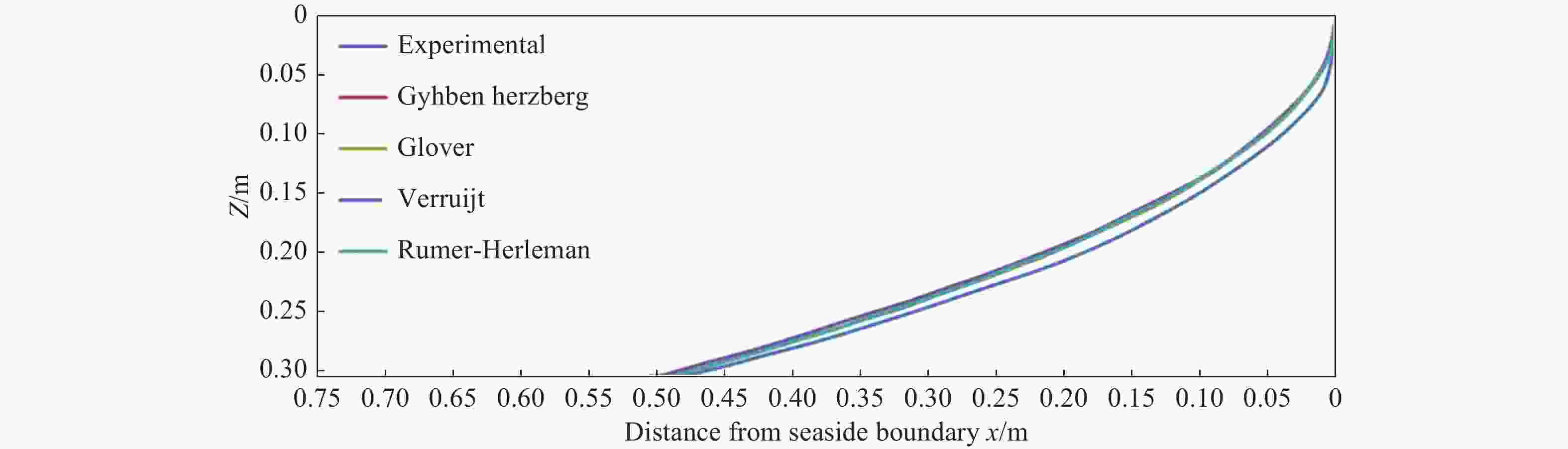
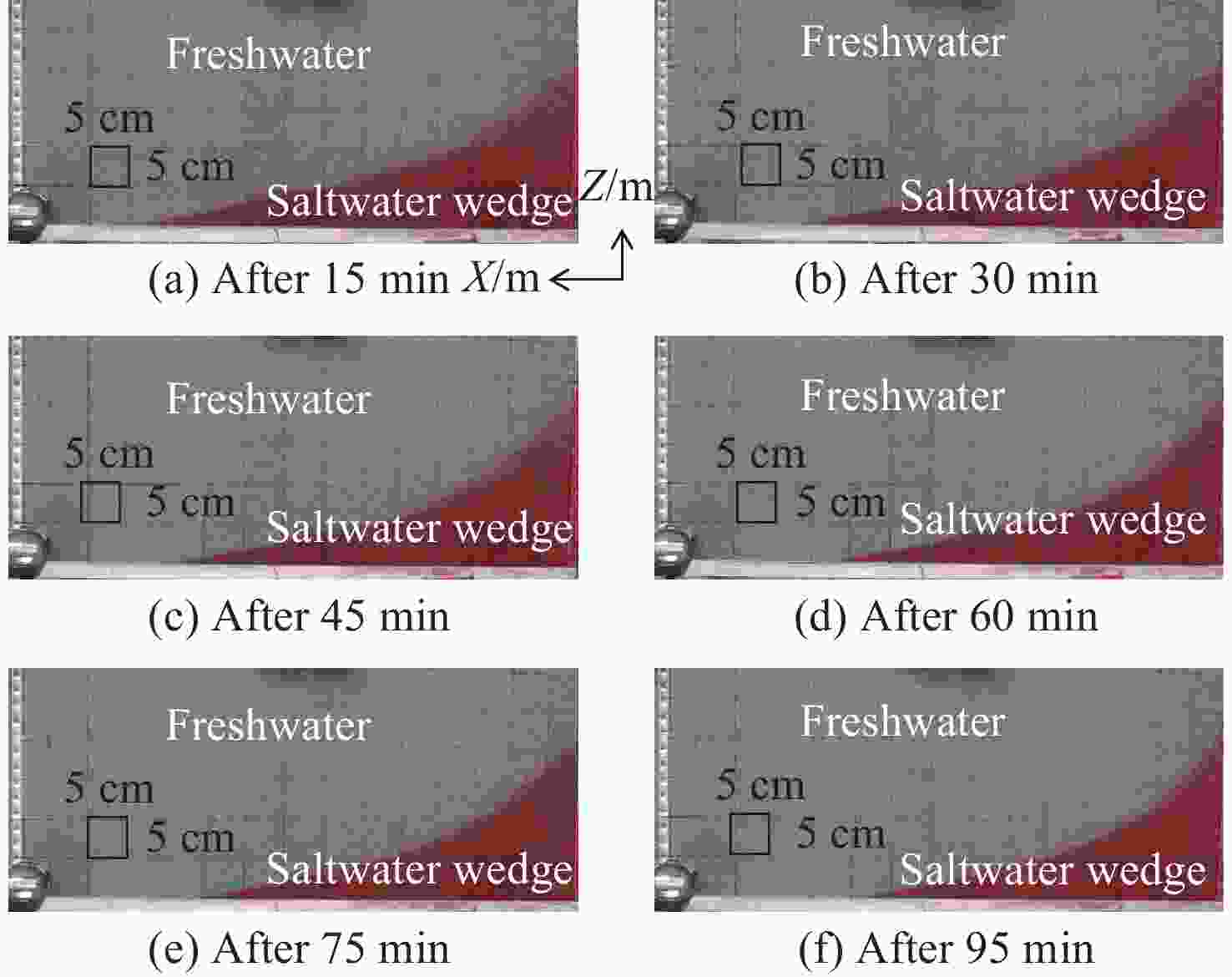
Figure 8. Comparison between the experimental SW- FW interface for the experimental unconfined coastal aquifer (from Armanuos, 2017) and the analytical solutions for Gyhben-Herzberg, Glover, Verruijt, and Rumer-Herleman through the web-based interface
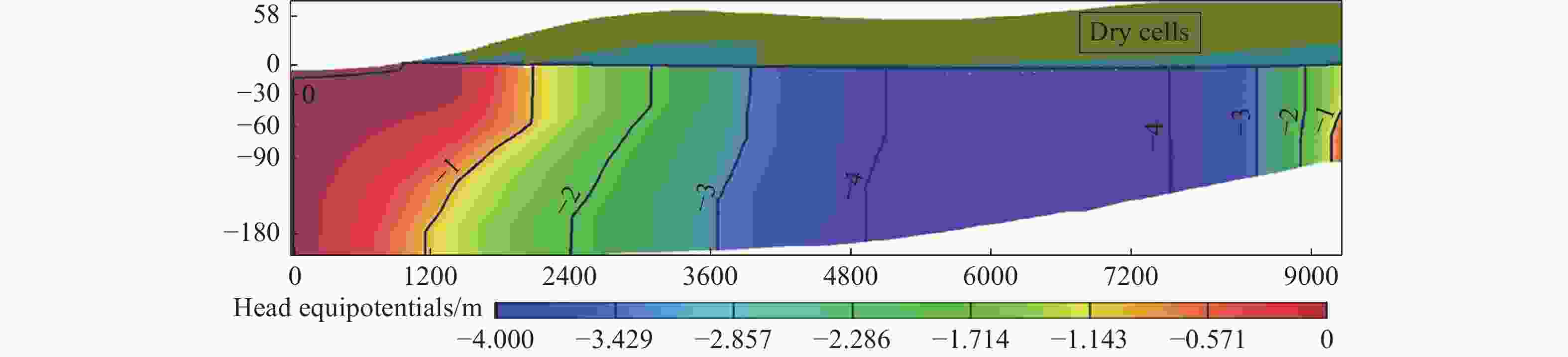
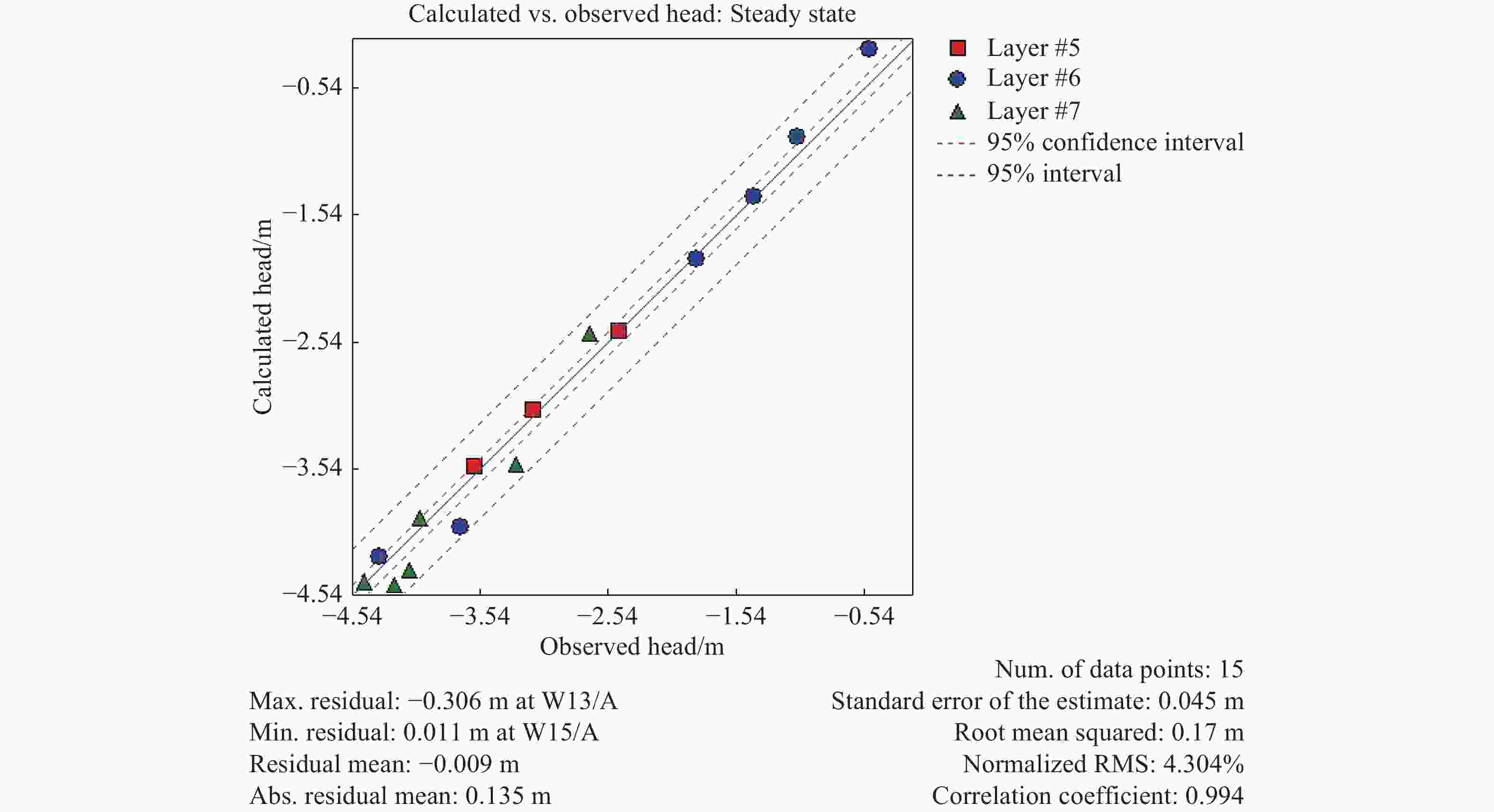
Figure 10. Calculated head versus observed head (Sirhan and Koch, 2013) for GCA
Figure 11. Simulated SI in Gaza aquifer for the base case. The contours represent the following concentration levels: 32,400 ppm for the 90% equi-concentration line, 18,000 ppm for the 50% equi-concentration line, and 3,600 ppm for the 10% equi-concentration line.
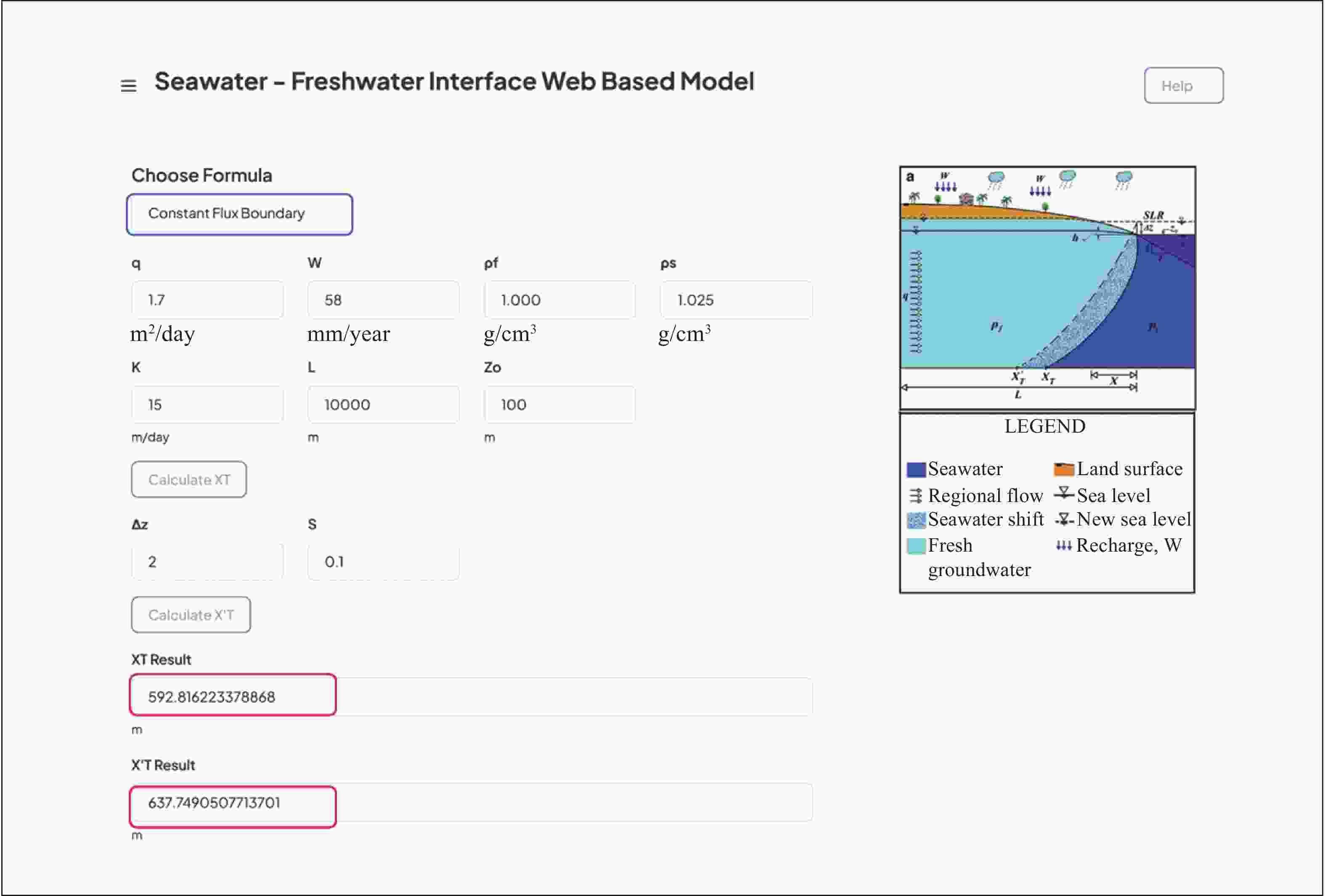
Figure 12. Input Parameters for calculating seawater intrusion wedge toe for the Gaza coastal aquifer using Ataie-Ashtiani et al. (2013) through the web-based interface tool for a constant flux boundary problem
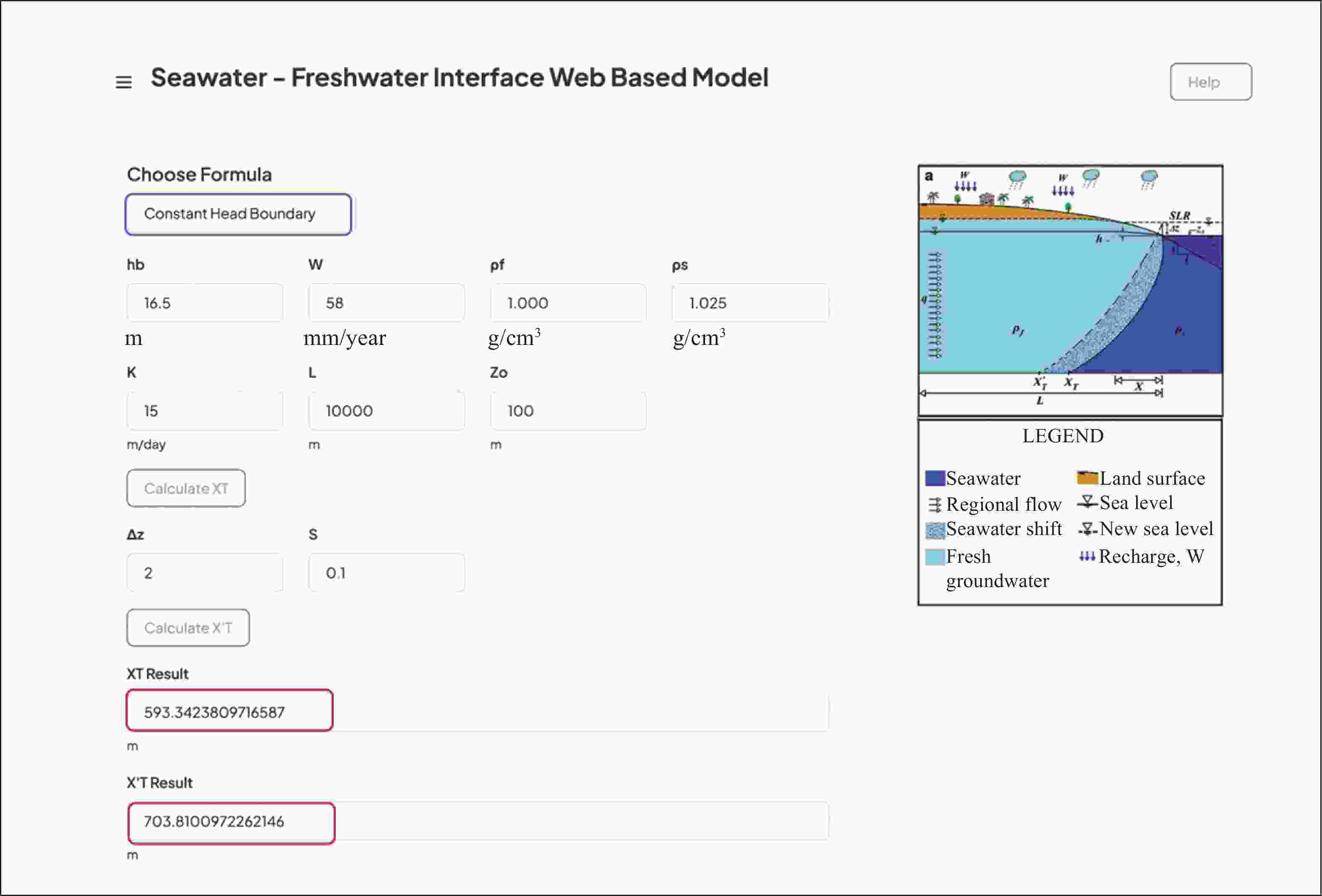
Figure 13. Input parameters for calculating seawater intrusion wedge toe for the Gaza coastal aquifer using Ataie-Ashtiani et al. (2013) through the web-based interface tool for a constant head boundary problem
Figure 14. Seawater intrusion distribution in the Gaza coastal aquifer: (a) steady-state condition, (b) SLR = 0.5 m, (c) SLR = 1.0 m, (d) SLR = 1.5 m, and (e) SLR = 2.0 m
Table 1. Analytical Equations implemented in the Seawater (SW)-Freshwater (FW) Interface Web-Based Model
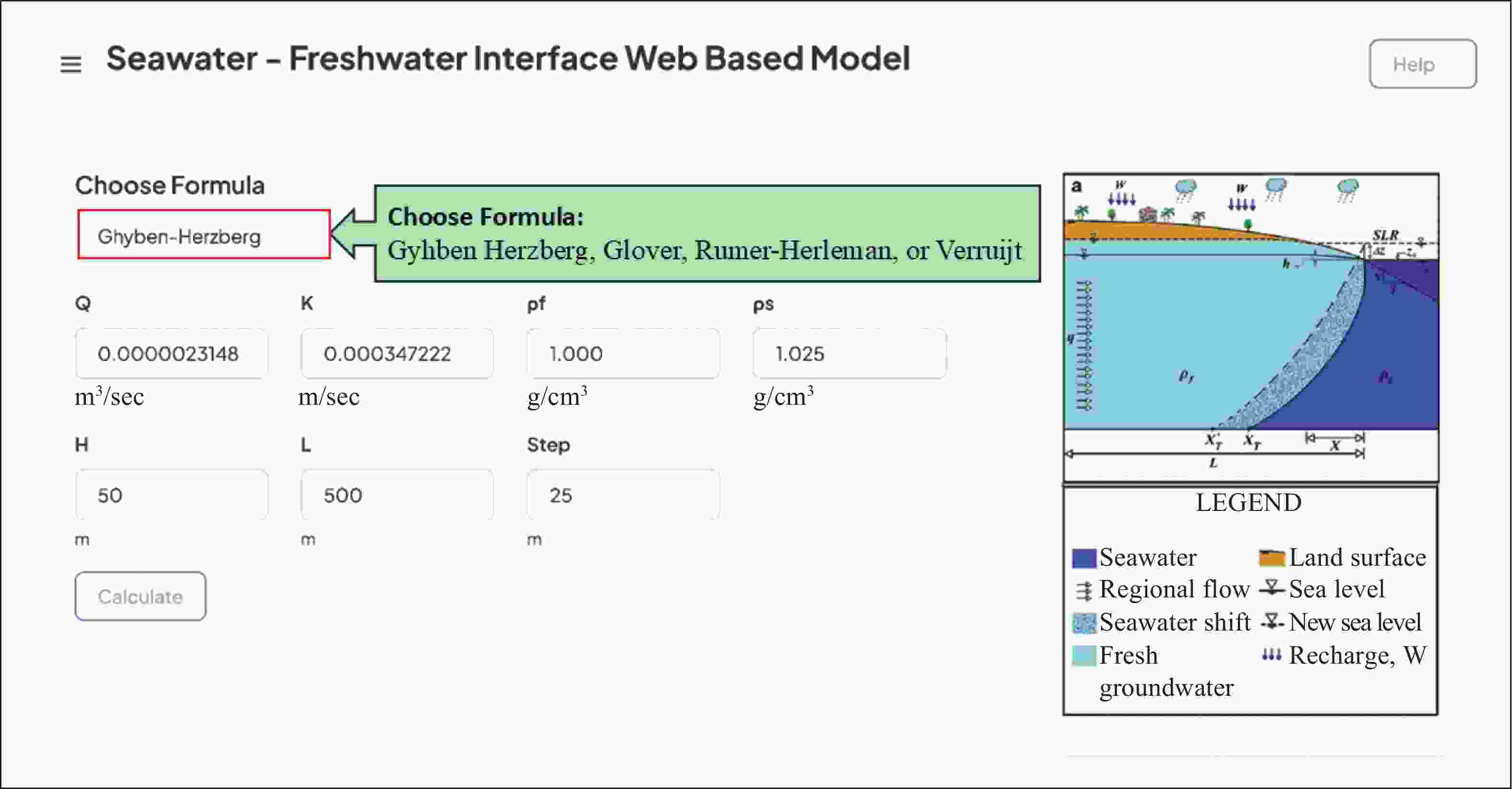
Seawater (SW)-Freshwater Interface Web-Based Model Analytical Equations Badon Ghyben (1888) & Herzberg (1901) $ \mathrm{z}=\dfrac{{\mathrm{\rho }}_{\mathrm{f}}}{{\mathrm{\rho }}_{\mathrm{s}}-{\mathrm{\rho }}_{\mathrm{f}}}{\mathrm{h}}_{\mathrm{f}} $ Glover (1959) $ {\mathrm{z}}^{2}=\dfrac{2{\mathrm{\rho }}_{\mathrm{f}}\mathrm{q}\mathrm{ }\mathrm{x}}{\mathrm{\Delta }\mathrm{\rho }\mathrm{ }\mathrm{K}}+{\left(\dfrac{{\mathrm{\rho }}_{\mathrm{f}}\mathrm{q}}{\mathrm{\Delta }\mathrm{\rho }\mathrm{ }\mathrm{K}}\right)}^{2} $ Rumer Jr and Harleman (1963) $ {\mathrm{z}}^{2}=\dfrac{2{\mathrm{\rho }}_{\mathrm{f}}\mathrm{q}\mathrm{ }\mathrm{x}}{\mathrm{\Delta }\mathrm{\rho }\mathrm{ }\mathrm{K}}+{0.55\left(\dfrac{{\mathrm{\rho }}_{\mathrm{f}}\mathrm{q}}{\mathrm{\Delta }\mathrm{\rho }\mathrm{ }\mathrm{K}}\right)}^{2} $ Verruijt (1968) $ \mathrm{Z}=-{\left({\left(\dfrac{\mathrm{q}}{\mathrm{\beta }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{K}}\right)}^{2}.\left(\dfrac{1-\mathrm{\beta }}{1+\mathrm{\beta }}\right)+2\left(\dfrac{\mathrm{q}}{\mathrm{\beta }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{K}}\right).\left(\dfrac{\mathrm{x}}{1+\mathrm{\beta }}\right)\right)}^{1/2} $ Where: $ {\rho }_{s} $ (M L−3) represents the seawater density, $ {\rho }_{f} $ (M L−3) represents the fresh groundwater density, $ {\textit{z}} $ (L) represents the depth to a point on the seawater-freshwater interface under the mean sea level, and $ {\mathrm{h}}_{\mathrm{f}} $ (L) represents the elevation of the water table in the aquifer measured above the mean sea level at the same point, q (L2 T−1) represents the rate of the fresh groundwater discharge, K (LT−1) denotes the hydraulic conductivity of the aquifer medium, $ \mathrm{\Delta }\mathrm{\rho }={\mathrm{\rho }}_{\mathrm{s}}-{\mathrm{\rho }}_{\mathrm{f}} $, x (L) represents the horizontal distance calculated from the shore line and $ \mathrm{\beta }=({\mathrm{\rho }}_{\mathrm{s}}-{\mathrm{\rho }}_{\mathrm{f}})/{\mathrm{\rho }}_{\mathrm{f}} $. 
下载: 导出CSV
Table 2. Analytical equations for the influence of Sea Level Rise (SLR) on Toe of Seawater (SW)-Freshwater (FW) Interface (Ataie-Ashtiani et al. 2013)
Constant Flux Boundary Steady-state SI toe $ {X}_{T}=\left(\dfrac{q}{W}+L\right)-\sqrt{{\left(\dfrac{q}{W}+L\right)}^{2}-\dfrac{K\delta (1+\delta ){{{\textit{z}}}_{o}}^{2}}{W}} $ Impact of SLR on the toe of SW-FW interface ${ {X}_{T}^{{\mathinner{\mkern2mu\raise1pt\hbox{.}\mkern2mu \raise4pt\hbox{.}\mkern2mu\raise7pt\hbox{.}\mkern1mu}} } }=\left(\dfrac{q}{W}+L-\dfrac{\Delta {\textit{z} } }{s}\right)-\sqrt{ {\left(\dfrac{q}{W}+L-\dfrac{\Delta {\textit{z} } }{s}\right)}^{2}-\dfrac{K\delta (1+\delta )({ { {\textit{z} } }_{o}+\Delta {\textit{z} })}^{2} }{W}+}\dfrac{\Delta {\textit{z} } }{s}$ Constant Head Boundary Steady state SI toe $ q=\dfrac{K({\left({h}_{b}+{{\textit{z}}}_{o}\right)}^{2}-\left(1+\delta \right){{{\textit{z}}}_{o}}^{2})}{2L}-\dfrac{WL}{2} $ $ {X}_{T}=\left(\dfrac{q}{W}+L\right)-\sqrt{{\left(\dfrac{q}{W}+L\right)}^{2}-\dfrac{K\delta (1+\delta ){{{\textit{z}}}_{o}}^{2}}{W}} $ Impact of SLR on toe of SW-FW interface $ q=\dfrac{K\left({\left({h}_{b}+{{\textit{z}}}_{o}\right)}^{2}-\left(1+\delta \right)\left({\textit{z}}+\Delta {\textit{z}}\right)^{2}\right)}{2\left(L-\dfrac{\Delta {\textit{z}}}{s}\right)}-\dfrac{W\left(L-\dfrac{\Delta {\textit{z}}}{s}\right)}{2} $ ${ {X}_{T}^{{{\mathinner{\mkern2mu\raise1pt\hbox{.}\mkern2mu \raise4pt\hbox{.}\mkern2mu\raise7pt\hbox{.}\mkern1mu}} } } }=\left(\dfrac{q}{W}+L-\dfrac{\Delta {\textit{z} } }{s}\right)-\sqrt{ {\left(\dfrac{q}{W}+L-\dfrac{\Delta {\textit{z} } }{s}\right)}^{2}-\dfrac{K\delta (1+\delta )({ { {\textit{z} } }_{o}+\Delta {\textit{z} })}^{2} }{W}+}\dfrac{\Delta {\textit{z} } }{s}$ Where: $ {X}_{T} $ (L) represents the position of the toe calculated from the sea boundary, z (L) represents the mean sea level rise, $ {{X}_{T}^{{\mathinner{\mkern2mu\raise1pt\hbox{.}\mkern2mu \raise4pt\hbox{.}\mkern2mu\raise7pt\hbox{.}\mkern1mu}}}} $ (L) represents the new position of the seawater-freshwater wedge toe calculated from the costal line boundary subsequently the Sea Level Rise (SLR), K (L T−1) represents the hydraulic conductivity of the groundwater aquifer system, L (L) represents the coastal aquifer length, q (L2 T−1) represents the fresh groundwater flow within the coastal aquifer boundary calculated per of the coastline aquifer unit width, zo (L) represents the coastal aquifer depth bottom calculated from the mean sea level, W (L T−1) represents the rate groundwater uniform recharge, and δ (−) represents the dimensionless value of the density term equal to (ρs–ρf)/ρf, where ρf (M L−3) is the density of the freshwater and ρs (M L−3) represents the density of the saltwater, s represents the slope of the seaward boundary of the aquifer. The public value of 0.025 is adopted for δ.
下载: 导出CSV
Table 3. Numerical model parameters for the hypothetical unconfined coastal aquifer (from Sun et al. 2021)
Parameter Description Value Units L Aquifer length 500 m H Aquifer depth 50 m n Porosity 0.30 -- K The hydraulic conductivity 30 m/d $ {\alpha }_{l} $ The longitudinal dispersivity 1.0 m $ {\alpha }_{t} $ The transverse dispersivity 0.1 m $ {\rho }_{f} $ The density of the fresh groundwater 1,000 Kg/m3 $ {\rho }_{s} $ The density of saline water 1,025 Kg/m3 Boundary condition hs Seawater hydraulic head 50 m qf Freshwater inflow 0.2 m/d Cs Saltwater concentration 35,000 mg/L Cf The concentration of the freshwater 1,000 mg/L
下载: 导出CSV
Table 4. Boundary conditions and hydraulic parameters used for Gaza aquifer model
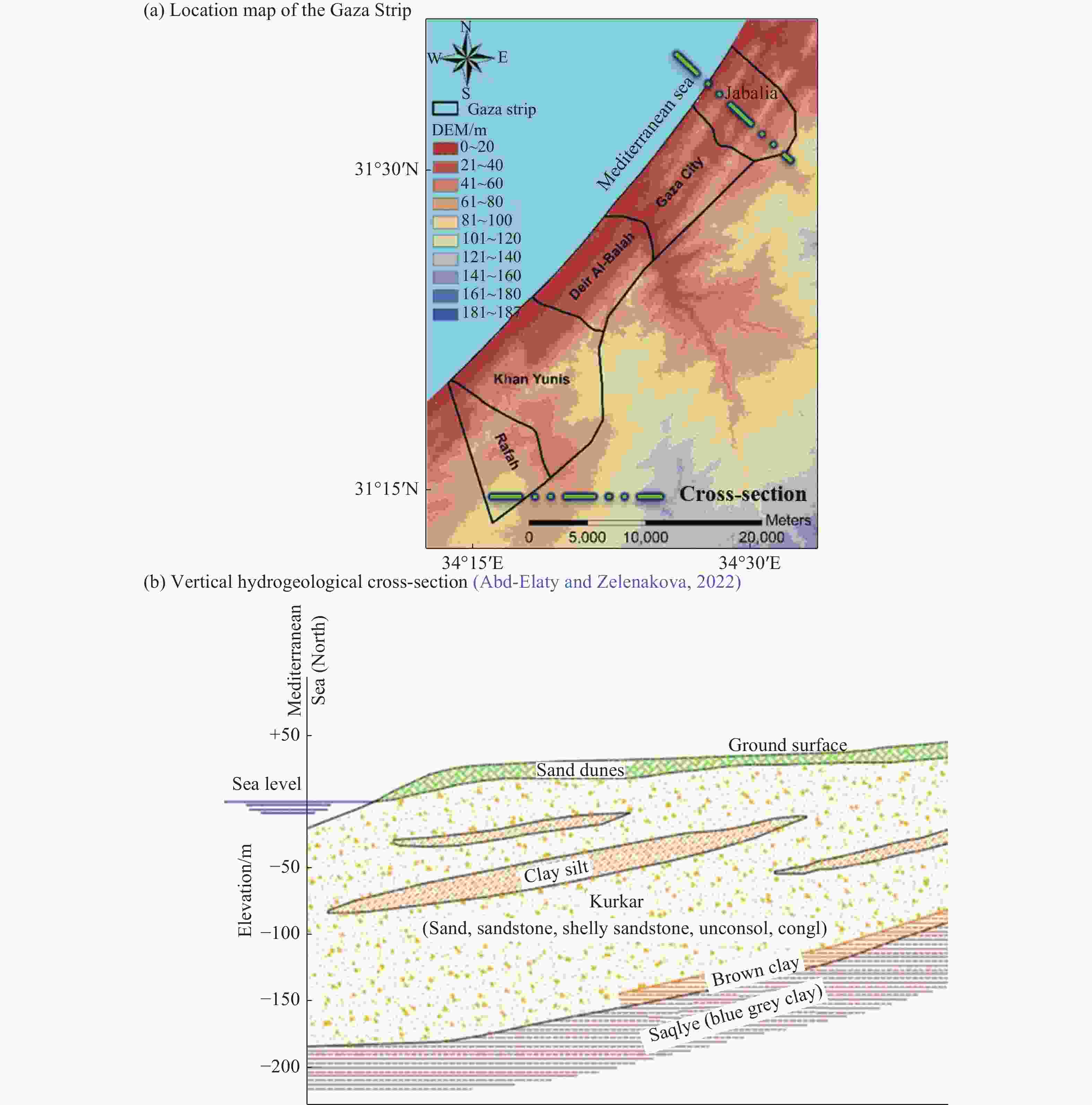
Boundary condition Value Unit The flux of the lateral freshwater 10 m3/d/m Well abstraction rates 20.75 m3/d/m Vertical recharge rate and the return flow 416.5 mm/year The head of the saltwater hs Zero m The concentration of the seaside boundary 35000 mg/L The concentration of the land side boundary 1000 mg/L Hydraulic parameters Confined aquifer Unconfined aquifer Unit The hydraulic conductivity in the horizontal (Kh) 0.2 34 m/d The hydraulic conductivity in the vertical direction (Kv) 0.02 3.4 m/d The value of the Effective porosity (ne) 0.3 0.25 - Total Porosity (nt) 0.45 0.35 - The density of the fresh groundwater 1000 1000 Kg/m3 The density of the saline water 1025 1025 Kg/m3 Specific storage 0.00001 0.0001 - Longitudinal dispersivity 50 12 - Transverse dispersivity 5 1.2 - Molecular diffusion coefficient (D) 0.0001 0.0001 m2/d
下载: 导出CSV
Table 5. Parameters for the Gaza Coastal Aquifer and comparison of SW-FW web-based toe position (for Zo = 100 m) with Ataie-Ashtiani et al. (2013)
No. K
(m/d)W
(mm/a)Zo (m) L (m) ∆Z S Flux BC Head BC Q (m2/d) XT
Ataie-Ashtiani et al. (2013)XT
Current
studyhb
(m)XT
Ataie-Ashtiani et al. (2013)XT
Current
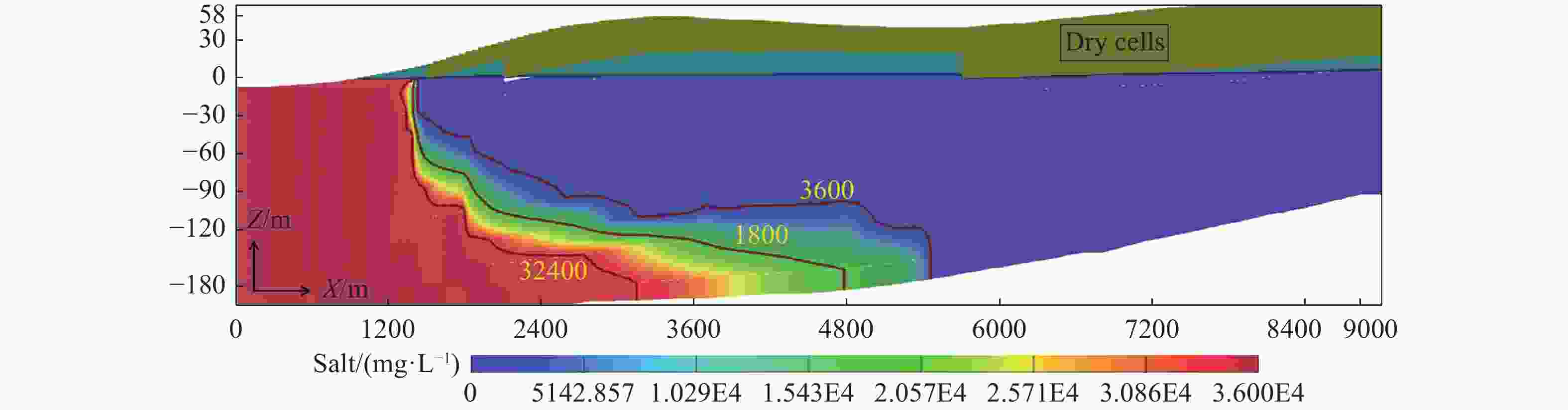
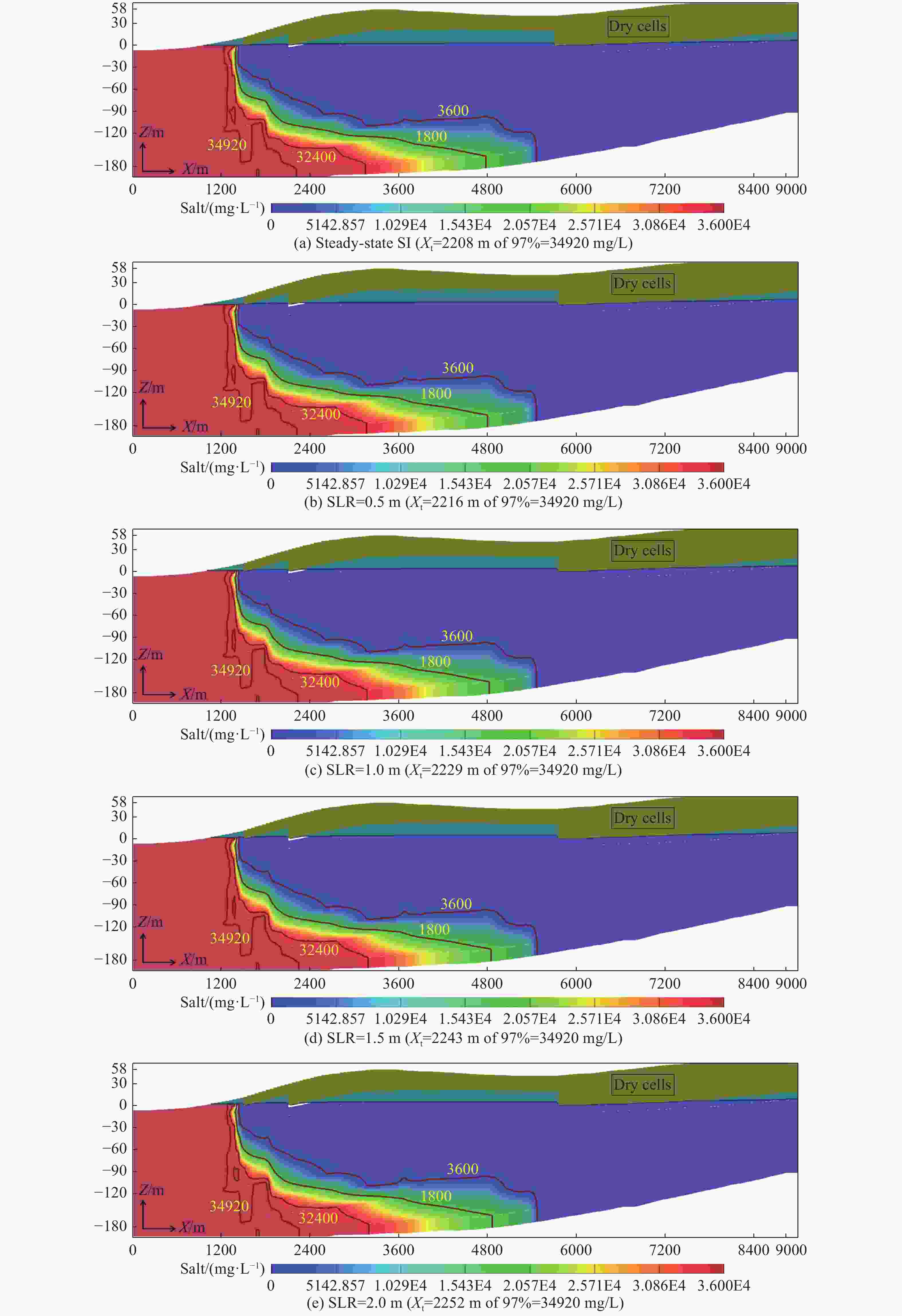
study1 15 58 100 10,000 0 - 1. 7 593 592.8 16.5 593 593.34 2 0.1 638 637.75 704 703.81 2 0.01 823 823.34 878 877.71 2 15 31 100 10,000 0 - 3.4 454 454.34 23.9 454 454.20 2 0.1 493 492.97 529 529.49 2 0.01 675 674.70 702 702.15 3 15 31 100 10,000 0 - 1.8 734 734.06 15 734 732.19 2 0.1 785 784.59 885 884.99 2 0.01 969 969.14 1055 1054.59
下载: 导出CSV
Table 6. Parameters for the Gaza Coastal Aquifer and comparison of SW-FW web-based toe position with SEAWAT results (for 90% concentration = 32,400 mg/L at Zo = 180 m) under various SLR scenarios
No. K (m/d) W (mm/a) Zo (m) L (m) ∆Z S Flux BC Q (m2/d) SEAWAT XT
Current
Study
(m)1 15 58 180 9,000 0 - 1.7 2,208 2,101 0.5 0.1 2,216 2,119 1.0 0.1 2,229 2,137 1.5 0.1 2,243 2,155 2.0 0.1 2,252 2,173
下载: 导出CSV
-
Abd-Elaty I, Zelenakova M. 2022. Saltwater intrusion management in shallow and deep coastal aquifers for high aridity regions. Journal of Hydrology: Regional Studies, 40: 101026. DOI: 10.1016/j.ejrh.2022.101026. Abdoulhalik A, Ahmed AA. 2017. The effectiveness of cutoff walls to control saltwater intrusion in multi-layered coastal aquifers: Experimental and numerical study. Journal of Environmental Management, 199: 62−73. DOI: 10.1016/j.jenvman.2017.05.040. Abualtayef M, Rahman GA, Snounu I, et al. 2017. Evaluation of the effect of water management interventions on water level of Gaza coastal aquifer. Arabian Journal of Geosciences, 10: 1−19. DOI: 10.1007/s12517-017-3329-x. Anderson EI. 2021. Analytical solutions for confined and unconfined coastal interface flow by the Hodograph method. Water Resources Research, 57(9). DOI: 10.1029/2021WR030323. Armanuos AM. 2017. Experimental and numerical study of saltwater intrusion in the Nile delta aquifer, Egypt [PhD Thesis]. Egypt-Japan University of Science and Technology (E-JUST). Armanuos AM, Al-Ansari N, Yaseen ZM. 2020a. Assessing the effectiveness of using recharge wells for controlling the saltwater intrusion in unconfined coastal aquifers with sloping beds: Numerical Study. Sustainability, 12(7): 2685. DOI: 10.3390/su12072685. Armanuos AM, Al-Ansari N, Yaseen ZM. 2020b. Underground barrier wall evaluation for controlling saltwater intrusion in sloping unconfined coastal aquifers. Water, 12(9): 2403. DOI: 10.3390/w12092403. Ataie-Ashtiani B, Werner AD, Simmons CT, et al. 2013. How important is the impact of land-surface inundation on seawater intrusion caused by sea-level rise? Hydrogeology Journal, 21(7): 1673. Chang SW, Clement TP, Simpson MJ, et al. 2011. Does sea-level rise have an impact on saltwater intrusion? Advances in Water Resources, 34(10): 1283–1291. DOI: 10.1016/j.advwatres.2011.06.006. Dang NM, Vien LN, Tung NB, et al. 2020. Assessments of climate change and sea level rise impacts on flows and saltwater intrusion in the Vu Gia—Thu Bon River Basin, Vietnam. APAC. Springer Singapore: 1367–1374. DOI: 10.1007/978-981-15-0291-0_185 Emara SR, Armanuos AM, Gado TA, et al. 2023a. Verification of experimental saltwater intrusion interface in unconfined coastal aquifers using numerical and analytical solutions. Acque Sotterranee - Italian Journal of Groundwater, 12(3): 23−38. DOI: 10.7343/as-2023-668. Emara SR, Armanuos AM, Shalby A. 2024a. Appraisal seawater intrusion vulnerability for the Moghra coastal aquifer, Egypt– application of the GALDIT index, sensitivity analysis, and hydro-chemical indicators. Groundwater for Sustainable Development, 25: 101166. DOI: 10.1016/j.gsd.2024.101166. Emara SR, Armanuos AM, Zeidan BA, et al. 2024b. Numerical investigation of mixed physical barriers for saltwater removal in coastal heterogeneous aquifers. Environmental Science and Pollution Research, 31(3): 4826−4847. DOI: 10.1007/s11356-023-31454-z. Emara SR, Gado TA, Zeidan BA, et al. 2023b. Evaluating the impact of inclined cutoff-wall to control seawater intrusion in heterogeneous coastal aquifers. Water Resources Management, 37(15): 6021−6050. DOI: 10.1007/s11269-023-03641-7. Fan Y, Lu W, Miao T, et al. 2020. Multiobjective optimization of the groundwater exploitation layout in coastal areas based on multiple surrogate models. Environmental Science and Pollution Research, 27(16): 19561−19576. DOI: 10.1007/s11356-020-08367-2. Ghyben BW. 1888. Nota in verband met de voorgenomen putboring nabij, Amsterdam. The Hague, 21. Glover RE. 1959. The pattern of fresh-water flow in a coastal aquifer. Journal of Geophysical Research, 64(4): 457−459. DOI: 10.1029/JZ064i004p00457. Goswami RR, Clement TP. 2007. Laboratory-scale investigation of saltwater intrusion dynamics. Water Resources Research, 43. DOI: 10.1029/2006WR005151. Guo W, Langevin CD. 2002. User's guide to SEAWAT; a computer program for simulation of three-dimensional variable-density ground-water flow (USGS Numbered Series No. 06-A7), User's guide to SEAWAT; a computer program for simulation of three-dimensional variable-density ground-water flow, Techniques of Water-Resources Investigations. DOI: 10.3133/twri06A7. Heen ZHA, Muhsen S. 2016. Application of vertical electrical sounding for delineation of sea water intrusion into the freshwater aquifer of southern governorates of Gaza Strip, Palestine. IUG Journal of Natural Studies, 24(2). Herzberg A. 1901. Die wasserversorgung einiger Nordseebader. Journal für Gasbeleuchtung und Wasserversorgung, 44: 842−844. Javadi A, Hussain M, Sherif M, et al. 2015. Multi-objective optimization of different management scenarios to control seawater intrusion in coastal aquifers. Water Resources Management, 29(6): 1843−1857. DOI: 10.1007/s11269-015-0914-1. Kaleris VK, Ziogas AI. 2013. The effect of cutoff walls on saltwater intrusion and groundwater extraction in coastal aquifers. Journal of Hydrology, 476: 370−383. DOI: 10.1016/j.jhydrol.2012.11.007. Koussis AD, Mazi K, Destouni G. 2012. Analytical single-potential, sharp-interface solutions for regional seawater intrusion in sloping unconfined coastal aquifers, with pumping and recharge. Journal of Hydrology, 416–417: 1–11. DOI: 10.1016/j.jhydrol.2011.11.012. Kuan WK, Jin G, Xin P, et al. 2012. Tidal influence on seawater intrusion in unconfined coastal aquifers. Water Resources Research, 48(2): 136−149. DOI: 10.1029/2011WR010678. Li Y, Wen MZ, Yu H, et al. 2024. Changes of coastline and tidal flat and its implication for ecological protection under human activities: Take China’s Bohai Bay as an example. China Geology, 7(1): 26−35. DOI: 10.31035/cg2023007. Lu C, Xin P, Li L, et al. 2015. Seawater intrusion in response to sea-level rise in a coastal aquifer with a general-head inland boundary. Journal of Hydrology, 522: 135−140. Lu C, Xin P, Kong J, et al. 2016. Analytical solutions of seawater intrusion in sloping confined and unconfined coastal aquifers. Water Resources Research, 52(9): 6989−7004. DOI: 10.1002/2016WR019101. Luo Z, Kong J, Shen C, et al. 2022. Approximate analytical solutions for assessing the effects of unsaturated flow on seawater extent in thin unconfined coastal aquifers. Advances in Water Resources, 160: 104104. DOI: 10.1016/j.advwatres.2021.104104. Mehdizadeh SS, Badaruddin S, Khatibi S. 2019. Abstraction, desalination and recharge method to control seawater intrusion into unconfined coastal aquifers. Global Journal of Environmental Science and Management, 5(1): 107−118. DOI: 10.22034/gjesm.2019.01.09. Motallebian M, Ahmadi H, Raoof A, et al. 2019. An alternative approach to control saltwater intrusion in coastal aquifers using a freshwater surface recharge canal. Journal of Contaminant Hydrology, 222: 56−64. DOI: 10.1016/j.jconhyd.2019.02.007. Qahman K. 2004. Aspects of hydrogeology, modeling, and management of seawater intrusion for Gaza aquifer–palestine. PhD. theis, LIMEN, Ecole Mohammadia D 'Ingenieurs, Université Mohammed V-Morocco. Ranjbar A, Mahjouri N, Cherubini C. 2020. Development of an efficient conjunctive meta-model-based decision-making framework for saltwater intrusion management in coastal aquifers. Journal of Hydro-Environment Research, 29: 45−58. DOI: 10.1016/j.jher.2019.11.005. Rumer Jr RR, Harleman DR. 1963. Intruded salt-water wedge in porous media. Journal of the Hydraulics Division, 89(6): 193−220. DOI: 10.1061/JYCEAJ.0000954. Sherif M, Sefelnasr A, Ebraheem AA, et al. 2014. Quantitative and qualitative assessment of seawater intrusion in Wadi Ham under different pumping scenarios. Journal of Hydrologic Engineering, 19(5): 855−866. DOI: 10.1061/(ASCE)HE.1943-5584.0000907. Sirhan H, Koch M. 2013. Numerical modeling of the effects of artificial recharge on hydraulic heads in constant-density ground water flow to manage the Gaza coastal aquifer, South Palestine. 6th International Conference on Water Resources and Environment Research, ICWRER: 3−7. Sun Q, Zheng T, Zheng X, et al. 2021. Effects of subsurface barriers on seawater intrusion and nitrate accumulation in coastal aquifers. Authorea Preprints. DOI: 10.22541/au.161252403.31172601. Verruijt A. 1968. A note on the Ghyben-Herzberg formula. Hydrological Sciences Journal, 13(4): 43−46. Wang XJ, Guo YF, Yu SC, et al. 2025. Nutrient dynamics and discharge in a coastal sandy beach aquifer. Hydrogeology & Engineering Geology, 52(1): 12−22. DOI: 10.16030/j.cnki.issn.1000-3665.202409063. Werner AD, Bakker M, Post VEA, et al. 2013. Seawater intrusion processes, investigation and management: Recent advances and future challenges. Advances in Water Resources, 51: 3−26. DOI: 10.1016/j.advwatres.2012.03.004. -
点击查看大图
计量
- 文章访问数: 111
- HTML全文浏览量: 55
- PDF下载量: 20
- 被引次数: 0
